Đề bài
Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Vẽ AH vuông góc với BC tại H. Cho biêý HB = HM. Chứng minh:
a) \(\Delta ABH = \Delta AMH\)
b) \(AG = \frac{2}{3}AB\)
Phương pháp giải - Xem chi tiết
- Kiểm tra ba cạnh tương ứng của hai tam giác ABH và tam giác AMH
- Sử dụng tính chất của ba đường trung tuyến
Lời giải chi tiết
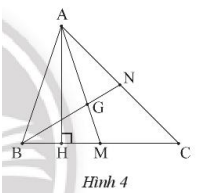
a) Ta có AH là trung trực của đoạn BM, suy ra AB = AM.
Xét hai tam giác ABH và AMH có:
Cạnh AH chung
HB = HM
AB = AM
Suy ra: \(\Delta ABH = \Delta AMH(c - c - c)\)
b) G là trọng tâm tam giác ABC.
Suy ra: \(AG = \frac{2}{3}AM\)
Theo câu a ta có: \(AB = AM\)
Suy ra: \(AG = \frac{2}{3}AB\)
