Đề bài
Vẽ hai góc kề bù \(\widehat {xOy}\),\(\widehat {yOz}\), biết \(\widehat {xOy}\) =130°. Gọi Ot là tia phân giác của \(\widehat {xOy}\) Tính \(\widehat {tOz}\).
Phương pháp giải - Xem chi tiết
Ta sử dụng tính chất tổng 2 góc kề bù bằng 180 độ và tính chất tia phân giác của một góc.
Lời giải chi tiết
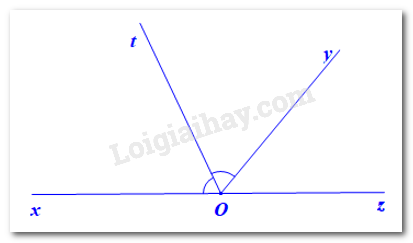
Vì Ot là tia phân giác của \(\widehat {xOy}\) nên:
\(\widehat {xOt}\)=\(\widehat {tOy}\)=\(\dfrac{1}{2}.\widehat {xOy}=\dfrac{1}{2}\).130°=65°.
Vì \(\widehat {xOt}\) và \(\widehat {tOz}\) là hai góc kề bù nên ta có:
\(\widehat {xOt}\)+\(\widehat {tOz}\)=180°
Suy ra \(\widehat {tOz}\)=180°−\(\widehat {xOt}\)=180°−65°=115°.
Vậy \(\widehat {tOz}\)=115°
