Đề bài
Cho đường tròn \((O, R)\), đường kính \(AB.\) Gọi \(C\) là điểm chính giữa của cung \(AB.\) Vẽ dây cung \(AB\). Vẽ dây \(CD\) dài bằng \(R.\) Tính góc ở tâm \(DOB.\) Có mấy đáp số?
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Trong tam giác đều mỗi góc bằng \(60^o\).
+) Số đo của nửa đường tròn bằng \(180^o.\)
Lời giải chi tiết
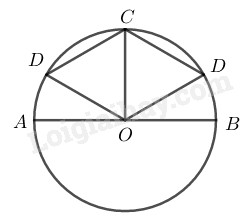
Điểm \(D\) có 2 trường hợp :
\(*)\) Nếu điểm \(D\) nằm giữa \(C\) và \(B\)
Ta có \(C\) điểm chính giữa của cung \(AB\) nên:
\(sđ\overparen{BC}= sđ \overparen{AC}= 90^o\)
Ta lại có \(CD = R\) \((gt)\)
Suy ra : \(OC = OD = CD = R\)
\( \Rightarrow \Delta OCD\) đều \( \Rightarrow \widehat {COD} = {60^o}\)
\( \Rightarrow sđ\overparen{CD}= \widehat{COD}=60^o\)
\( \Rightarrow sđ \overparen{BD} = sđ \overparen{BC} - sđ \overparen{CD}\)\( = {90^o} - {60^o} = {30^o}\)
Suy ra \(\widehat {BOD} = sđ \overparen{BD} = 30^o\)
\(*)\) Nếu \(D\) nằm giữa \(C\) và \(A\) ta có : \(CD = OC = OD = R\)
\( \Rightarrow \Delta OCD\) đều \( \Rightarrow \widehat {COD} = {60^o}\)
\(sđ \overparen{CD} = \widehat{COD} = 60^o\)
\(sđ \overparen{BD} = sđ \overparen{BC} + sđ \overparen{CD}\)\(= {90^o} + {60^o} = {150^o}\)
Suy ra \(\widehat {BOD}= sđ \overparen{BD} = 150^o\)
soanvan.me
