Đề bài
Trên một đường tròn, có cung \(AB\) bằng \(140^o,\) cung \(AD\) nhận \(B\) làm điểm chính giữa, cung \(CB\) nhận \(A\) là điểm chính giữa. Tính số đo cung nhỏ \(CD\) và cung lớn \(CD.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Số đo của cung lớn bằng hiệu giữa \(360^o\) và số đo cung nhỏ (có chung hai đầu mút với cung lớn).
Lời giải chi tiết
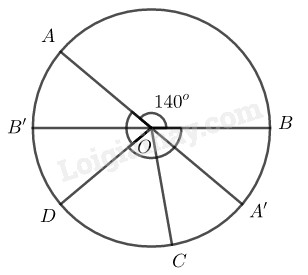
Vì cung \(AD\) nhận \(B\) làm điểm chính giữa, cung \(CB\) nhận \(A\) là điểm chính giữa nên \(\overparen{AB} = \overparen{BD} = \overparen{AC}\)
\( \Rightarrow \widehat {AOB} = \widehat {BOD} = \widehat {AOC} = {140^0}\)
Kẻ đường kính \(AA’, BB’\) ta có:
\(\widehat {AOB} + \widehat {AOB'} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {AOB'} = {180^0} - \widehat {AOB} \)\(= {180^0} - {140^0} = {40^0}\)
Suy ra: \(\widehat {BOA'} = \widehat {AOB'} = {40^0}\) (hai góc đối đỉnh)
\(\widehat {B'OD} + \widehat {BOD} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {B'OD} = {180^0} - \widehat {BOD}\)\( = {180^0} - {140^0} = {40^0}\)
\(\widehat {AOC} = \widehat {AOB'} + \widehat {B'OD} + \widehat {DOC}\)
\( \Rightarrow \widehat {DOC} = \widehat {AOC} - \widehat {AOB'} - \widehat {B'OD}\)\( = {140^0} - {40^0} - {40^0} = {60^0}\)
\(sđ \overparen{CD} (nhỏ) = \widehat {COD} = {60^0}\)
\(sđ \overparen{CD} (lớn) =360^o- sđ \overparen{CD} (nhỏ)\)\( = 360^o-60^o = 300^o\)
soanvan.me
