Video hướng dẫn giải
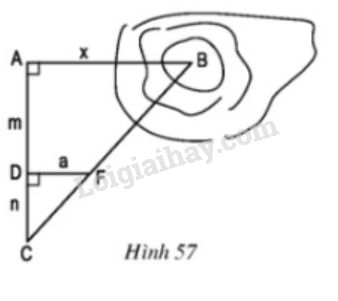
Để đo khoảng cách giữa hai điểm \(A\) và \(B\), trong đó \(B\) không tới được, người ta tiến hành đo và tính khoảng cách như hình 57:
\(AB // DF; AD = m; DC = n; DF = a\).
LG a.
Em hãy nói rõ về cách đo như thế nào.
Phương pháp giải:
Nhìn hình để suy ra được cách đo.
Lời giải chi tiết:
Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
LG b.
Tính độ dài \(x\) của khoảng cách \(AB\).
Phương pháp giải:
Áp dụng:
- Tính chất 2 tam giác đồng dạng.
- Định lí: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết:
Có \(DF // AB\) (cùng vuông góc với AC theo cách dựng) nên \(∆CDF ∽ ∆CAB\)
\( \Rightarrow \dfrac{DF}{AB}=\dfrac{CD}{CA}\) (tính chất 2 tam giác đồng dạng)
\( \Rightarrow AB = \dfrac{DF.CA}{CD}= \dfrac{a(m+n)}{n}\)
Vậy \(x= \dfrac{DF.CA}{CD}= \dfrac{a(m+n)}{n}\)
soanvan.me
