Đề bài
Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước \(AC\) được chia đến \(1\) mm và gắn với một kim loại hình tam giác \(ABD\), khoảng cách \(BC= 10\) cm.
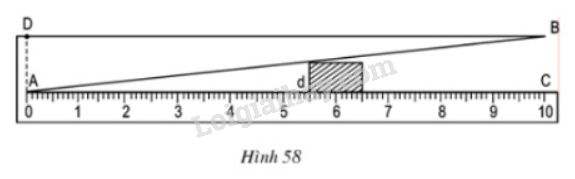
Muốn đo bề dầy của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt thước \(AC\)), khi đó trên thước \(AC\) ta đọc được bề dày \(d\) của vật (trên hình vẽ ta có \(d=5,5mm\)).
Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi vạch trên thước \(AC\) (\(d ≤ 10\) mm).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng
- Tính chất hai tam giác đồng dạng
- Định lí: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
Lời giải chi tiết
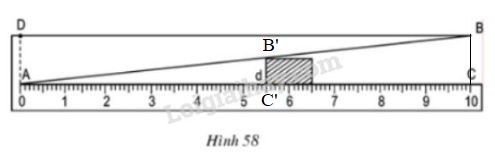
Theo hình vẽ thì \(B'C'//BC\) nên \(∆ABC ∽ ∆AB'C'\) (theo định lí)
\( \Rightarrow \dfrac{AC'}{AC}= \dfrac{B'C'}{BC}\)
\(B'C'\) là bề dày của vật cần đo
Vì \(d ≤ 10\) mm nên \(BC=10mm=1cm\)
\( \Rightarrow B'C' = \dfrac{AC'. BC}{AC}= \dfrac{1}{10}AC'\)
Vậy khi \(AC' = 5,5 \,cm\) thì đọc \(B'C' = \dfrac{1}{10}. 5,5\, cm\)\(=0,55cm = 5,5\, mm.\)
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì cạnh tương ứng tỉ lệ.
soanvan.me
