Đề bài
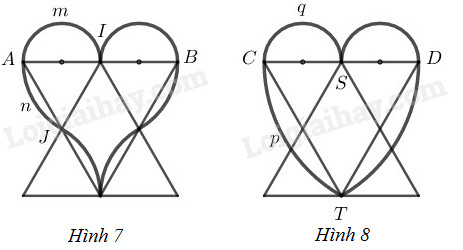
Các tam giác trong hai hình quả tim dưới đây \((h.7\) và \(h.8)\) đều là tam giác đều. Biết \(AB = CD = 8cm.\) Tính chu vi của mỗi hình quả tim.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức: Độ dài \(C\) của một đường tròn bán kính \(R\) được tính theo công thức: \(C=2\pi R.\) Nếu gọi \(d\) là đường kính đường tròn \((d=2R)\) thì \(C=\pi d.\)
Lời giải chi tiết
Hình \(7\) có \(2\) nửa đường tròn đường kính \(4 cm\) và có 4 cung có độ dài là \(\displaystyle {1 \over 6}\) đường tròn bán kính \(4 cm\)
\(\overparen{AmI}\) là nửa đường tròn đường kính \(4 cm\), gọi độ dài cung này là \({l_1}\), có 2 cung như thế.
\({l_1} = \displaystyle {1 \over 2}\pi .4 = 2\pi \) (cm)
\(\overparen{AnJ}\) là cung \(\displaystyle {1 \over 6}\) đường tròn bán kính \(4 cm\) (trên hình 7 có \(4\) cung bằng nhau (vì \(4\) đường tròn đó có cùng bán kính))
Gọi \(\overparen{AnJ}\) có độ dài \({l_2}\)
\({l_2} = \displaystyle {1 \over 6}.2\pi .4 = {4 \over 3}\pi \) \((cm)\)
Chu vi hình \(7\) là: \(2.{l_1} + 4.{l_2}\)\(=2\pi .2 + \displaystyle {4 \over 3}\pi .4 = \displaystyle {{28} \over 3}\pi \) \((cm)\)
Hình \(8\) có hai nửa đường tròn đường kính \(4 cm\) và hai cung \(\displaystyle {1 \over 6}\) đường tròn bán kính \(8 cm\)
Cung \(\overparen{CpS}\) là nửa đường tròn đường kính \(4 cm\) có độ dài \({l_1}\)
\({l_1} = \displaystyle {1 \over 2}.\pi .4 = 2\pi \) (cm)
Cung \(\overparen{CqT}\) là \(\displaystyle {1 \over 6}\) đường tròn bán kính \(8 cm\) có độ dài \({l_2}\)
\({l_2} = \displaystyle {1 \over 6}.2\pi .8 = {8 \over 3}\pi \) \((cm)\)
Chu vi hình \(8\) bằng: \(2.{l_1} + 2.{l_2} = 2.2\pi + 2.\displaystyle {8 \over 3}\pi =\displaystyle {{28} \over 3}\pi \) \((cm)\)
soanvan.me
