Đề bài
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng thay đổi đi qua A cắt (O) ở A và M, cắt (O’) tại A và M’. Gọi P và P’ lần lượt là trung điểm của AM và AM’.
a) Tìm quỹ tích trung điểm I của đoạn thẳng PP’.
b) Tìm quỹ tích trung điểm J của đoạn thẳng MM’.
Lời giải chi tiết
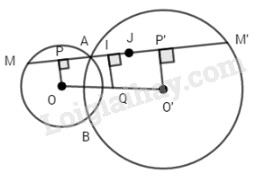
a) Gọi Q là trung điểm của OO’ thì QI\( \bot \)IA. Suy ra quỹ tích I là đường tròn đường kính AQ.
b) Vì J là trung điểm MM’ nên
\(\overrightarrow {AJ} = {1 \over 2}\left( {\overrightarrow {AM} + \overrightarrow {AM'} } \right)\)
\( = \overrightarrow {AP} + \overrightarrow {AP'} = 2\overrightarrow {AI} \)
Vậy phép vị tự tâm A tỉ số 2 biến điểm I thành điểm J. Do đó, quỹ tích J là ảnh của đường tròn đường kính AQ qua phép vị tự đó.
soanvan.me
