Đề bài
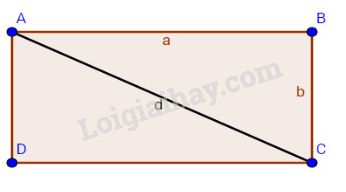
Điền vào chỗ trống, biết rằng \(a, b\) là độ dài các cạnh, \(d\) là độ dài đường chéo của một hình chữ nhật.
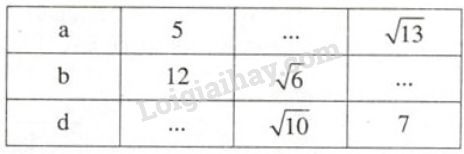
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lý Pytago.
Lời giải chi tiết
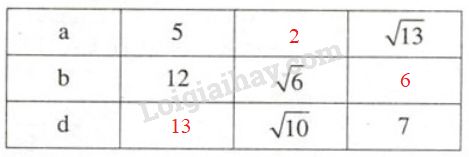
Cột thứ hai:
Áp dụng định lí Pytago vào tam giác vuông \(ABC\) có \( \widehat {ABC} = {90^o},\) ta có:
\({d^{2}} = {\rm{ }}{a^2} + {\rm{ }}{b^2} = {\rm{ }}{5^2} + {\rm{ }}{12^2} = {\rm{ }}25{\rm{ }} + {\rm{ }}144{\rm{ }}\)\( = {\rm{ }}169\)
Nên \(d =\sqrt{169}= 13\)
Cột thứ ba:
Áp dụng định lí Pytago vào tam giác vuông \(ABC\) có \( \widehat {ABC} = {90^o},\) ta có:
\({a^2} + {\rm{ }}{b^{2}} = {d^2} \)
\(\Rightarrow {a^2} = {\rm{ }}{d^2} - {b^2} = {\left( {\sqrt {10} } \right)^2} - {\left( {\sqrt 6 } \right)^2}\)
\(= 10 - 6 = 4\Rightarrow a = \sqrt 4=2\)
Cột thứ tư:
Áp dụng định lí Pytago vào tam giác vuông \(ABC\) có \( \widehat {ABC} = {90^o},\) ta có:
\({a^2} + {\rm{ }}{b^{2}} = {\rm{ }}{d^2}\)
\(\Rightarrow {b^2} = {\rm{ }}{d^2} - {\rm{ }}{a^2} = {\rm{ }}{7^2} -{\left( {\sqrt {13} } \right)^2}\)
\(= 49 - 13 = 36\Rightarrow b=\sqrt {36}= 6\)
soanvan.me
