Video hướng dẫn giải
Các câu sau đúng hay sai ?
LG a.
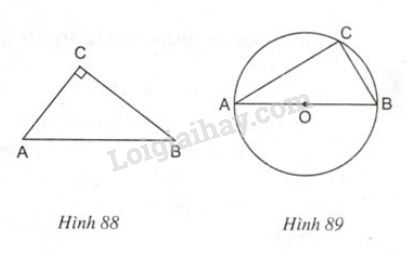
Nếu tam giác \(ABC\) vuông tại \(C\) thì điểm \(C\) thuộc đường tròn có đường kính là \(AB\) (h.\(88\))
Phương pháp giải:
Áp dụng tính chất: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Lời giải chi tiết:
Đúng.
Gọi \( O\) là trung điểm của \(AB.\) Ta có \(CO\) là trung tuyến ứng với cạnh huyền \(AB\) của tam giác vuông \(ACB\)
\( \Rightarrow OC = \dfrac{1}{2}AB\) hay \(OC = OA = OB\) (Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy)
Nên \(A, B, C\) cùng thuộc đường tròn bán kính \(OA\). Vậy \(C\) thuộc đường tròn đường kính \(AB\).
LG b.
Nếu điểm \(C\) thuộc đường tròn có đường kính là \(AB\) (\(C\) khác \(A\) và \(B\)) thì tam giác \(ABC\) vuông tại \(C\) (h.\(89\)).
Phương pháp giải:
Áp dụng tính chất: Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
Lời giải chi tiết:
Đúng.
Gọi \(O\) là tâm đường tròn. Suy ra \(CO = AO = OB\) (= bán kính) mà \(AB\) là đường kính nên \(AB=2R\)
Suy ra \(CO = AO = OB=\dfrac{AB}2\)
Tam giác \(ABC\) có trung tuyến \(CO\) và \(CO\) bằng nửa cạnh \(AB\) (chứng minh trên ) nên tam giác \(ABC\) vuông tại \(C\) (trong tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông).
soanvan.me
