Trên nửa đường tròn đường kính AB = 2R, lấy một điểm C tùy ý (C khác A, B). Kẻ \(CH \bot AB\left( {H \in AB} \right)\), gọi \(I\) là trung điểm của CH.
Trên nửa đường thẳng \(It\) vuông góc với \(mp\left( {ABC} \right)\), lấy điểm S sao cho \(\widehat {ASB}={90^0}.\)
LG 1
Chứng minh rằng khi C chạy trên nửa đường tròn đã cho thì :
a) Mặt phẳng (SAB) cố định ;
b) Điểm cách đều các điểm S, A, B, I chạy trên một đường thẳng cố định.
Lời giải chi tiết:
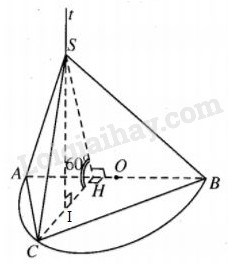
a) Do các tam giác ASB và ACB vuông nên :
\(S{H^2} = AH.BH;\;C{H^2} = AH.BH.\)
Vậy SH=CH. Mặt khác \(SI \bot CH\) và CI=IH nên SC=SH.
Vậy tam giác SCH đều, suy ra \(\widehat {SHI} = {60^0}\)
Mặt khác, ta có \(AB \bot HI,AB \bot SH\)
\( \Rightarrow \) \(\widehat {SHI}\) là góc giữa hai mặt phẳng (SAB) và (ABC).
Vậy mặt phẳng (SAB) qua AB cố định và tạo với mặt phẳng cố định (ABC) một góc 600 nên nó phải cố định.
b) Gọi K là điểm cách đều các điểm S, A, B, I.
Do K cách đều ba điểm S, A, B nên nó phải thuộc đường thẳng \(\Delta \) vuông góc với mặt phẳng (SAB) tại trung điểm O của AB cố định nên đường thẳng \(\Delta \) cố định.
Vậy K thuộc đường thẳng \(\Delta \) cố định.
LG 2
Cho AH = x. Tính thể tích khối chóp S.ABC theo R và x. Tìm vị trí của C để thể tích đó lớn nhất.
Lời giải chi tiết:
Trong tam giác ABC ta có :
\(C{H^2} = HA.HB \Rightarrow CH = \sqrt {x\left( {2R - x} \right)} \)
Do tam giác SCH đều nên \(SI = {{CH\sqrt 3 } \over 2} = {{\sqrt 3 } \over 2}\sqrt {x\left( {2R - x} \right)} \)
Vậy: \({V_{S.ABC}} = {1 \over 3}.{1 \over 2}.AB.CH.SI = {{R\sqrt 3 } \over 6}x(2R - x)\)
\({V_{S.ABC}}\) lớn nhất \( \Leftrightarrow x\left( {2R - x} \right)\) lớn nhất \( \Leftrightarrow x = \left( {2R - x} \right)\) \((do\,\,x + \left( {2R - x} \right) = 2R\, \text{không đổi })\) \( \Leftrightarrow x = R \Leftrightarrow C\) là điểm chính giữa của cung AB.
soanvan.me
