Cho hình tứ diện ABCD.
LG 1
Chứng minh rằng nếu chân H của đường cao hình tứ diện xuất phát từ A trùng với trực tâm của tam giác BCD và nếu \(AB \bot AC\) thì \(AC \bot AD\) và \(AD \bot AB.\)
Lời giải chi tiết:
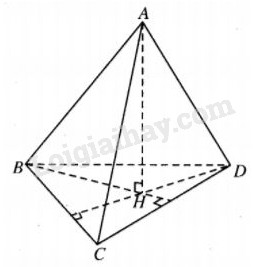
Do H là trực tâm \(\Delta BCD\) nên \(BH \bot CD.\)
Mặt khác \(AH \bot (BCD)\) nên \(AH \bot CD.\)
Vậy \(CD \bot (ABH) \Rightarrow CD \bot AB.\)
Cùng với giả thiết \(AC \bot AB\), ta suy ra \(AB \bot (ACD) \Rightarrow AB \bot AD.\)
Tương tự \(AC \bot AD.\)
LG 2
Giả sử BC = CD = DB, AB = AC = AD. Gọi H là chân đường cao của hình tứ diện xuất phát từ A, J là chân của đường vuông góc hạ từ H xuống AD. Đặt AH = h, HJ = d. Tính thể tích của hình tứ diện ABCD theo d và h.
Lời giải chi tiết:
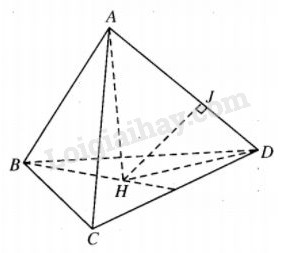
Từ AB = AC = AD suy ra HB = HC = HD, tức H là tâm đường tròn ngoại tiếp tam giác BCD.
Xét tam giác vuông AHD, ta có :
\(\eqalign{ & {1 \over {H{J^2}}} = {1 \over {A{H^2}}} + {1 \over {H{D^2}}} \cr & \Rightarrow {1 \over {H{D^2}}} = {1 \over {{d^2}}} - {1 \over {{h^2}}} \cr & \Rightarrow HD = {{hd} \over {\sqrt {{h^2} - {d^2}} }}. \cr} \)
Do tam giác BCD đều nên \(DH = BC.{{\sqrt 3 } \over 3},\) hay \(BC = DH\sqrt 3 .\)
Vậy \(V = {1 \over 3}{S_{BCD}}.AH = {{\sqrt 3 {d^2}{h^3}} \over {4\left( {{h^2} - {d^2}} \right)}}.\)
soanvan.me
