Đề bài
Hình chóp đều \(S.ABC\) có cạnh đáy \(a = 12cm\), chiều cao \(h = 8cm.\) Hãy tính diện tích xung quanh của hình chóp đó.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn.
\({S_{xq}} = pd\)
Trong đó: \(p\): nửa chu vi đáy
\(d\): trung đoạn của hình chóp đều
- Định lí Pytago trong tam giác vuông: Bình phương của cạnh huyền bằng tổng các bình phương của các cạnh góc vuông.
Lời giải chi tiết
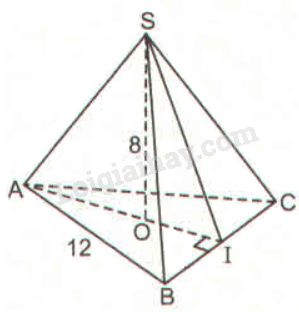
Gọi \(SO\) là đường cao của hình chóp \(S.ABC\) (\(O\) là trọng tâm của tam giác \(ABC)\)
Kẻ \(AO\) kéo dài cắt \(BC\) tại \(I\). Suy ra \(I\) là trung điểm của \(BC.\)
Ta có \(AI ⊥ BC\) (tính chất tam giác đều)
\(BI = IC = \displaystyle {1 \over 2}BC=6\,(cm)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(AIB\), ta có:
\(A{B^2} = B{I^2} + A{I^2}\)
\( \Rightarrow A{I^2} = A{B^2} - B{I^2} \)
\( \Rightarrow A{I^2}= {12^2} - {6^2} = 108 \)
\( \Rightarrow AI = \sqrt {108} \,(cm) \)
Vì \(O\) là trọng tâm của tam giác \(ABC\) nên ta có: \(OI = \displaystyle{1 \over 3}AI = {1 \over 3}\sqrt {108} \;(cm)\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(SOI\), ta có:
\(\displaystyle S{I^2} = S{O^2} + O{I^2} = {8^2} + {1 \over 9}.108\)\(\, = 76 \)
\( \Rightarrow SI = \sqrt {76} \;(cm) \)
Diện tích xung quanh của hình chóp là:
\({S_{xq}} = pd ={\dfrac{1}{2}.{12.3} } .\sqrt {76} \)\(\,= 18\sqrt {76}\;(c{m^2})\).
soanvan.me
