Đề bài
Cho đường tròn tâm O, hai dây CD và EF bằng nhau và vuông góc với nhau tại I. Biết IC = 2 cm, ID = 4 cm. Tính khoảng cách từ O đến dây EF.
Phương pháp giải - Xem chi tiết
+) Kẻ \(OH \bot EF,\,\,OK \bot CD\). Chứng minh tứ giác OHIK là hình vuông.
+) Chứng minh K là trung điểm của CD. Cộng trừ đoạn thẳng, tính KI.
Lời giải chi tiết
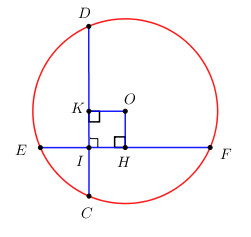
Kẻ \(OH \bot EF,\,\,OK \bot CD\).
Xét tứ giác OHIK có : \(\widehat {OHI} = \widehat {OKI} = \widehat {HIK} = {90^0} \Rightarrow \) Tứ giác \(OHIK\) là hình chữ nhật (tứ giác có 3 góc vuông).
Lại có \(EF = CD \Rightarrow OH = OK\) (trong một đường tròn, hai dây bằng nhau thì cách đều tâm)
\( \Rightarrow OHIK\) là hình vuông (Hình chữ nhật có 2 cạnh kề bằng nhau) \( \Rightarrow OH = KI\).
Ta có \(CD = IC + ID = 2 + 4 = 6\,\,\left( {cm} \right)\).
\(OK \bot CD \Rightarrow K\) là trung điểm của CD \( \Rightarrow KC = KD = \dfrac{1}{2}CD = 3\,\,\left( {cm} \right)\).
Vậy \(KI = KC - IC = 3 - 2 = 1\,\,\left( {cm} \right)\).
soanvan.me
