Đề bài
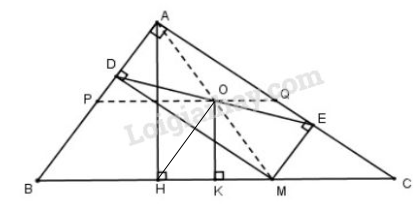
Cho tam giác \(ABC\) vuông tại \(A\). Lấy \(M\) là một điểm bất kì thuộc cạnh \(BC\). Gọi \(MD\) là đường vuông góc kẻ từ \(M\) đến \(AB\), \(ME\) là đường vuông góc kẻ từ \(M\) đến \(AC\), \(O\) là trung điểm của \(DE\).
a) Chứng mình rằng ba điểm \(A, O, M\) thẳng hàng.
b) Khi điểm \(M\) di chuyển trên cạnh \(BC\) thì điểm \(O\) di chuyển trên đường nào ?
c) Điểm \(M\) ở vị trí nào trên cạnh \(BC\) thì \(AM\) có độ dài nhỏ nhất?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Đường trung bình của tam giác thì song song với cạnh thứ 3 và bằng nửa độ dài cạnh ấy.
+) Dấu hiệu nhận biết hình chữ nhật là tứ giác có ba góc vuông.
Lời giải chi tiết
a) Tứ giác \(ADME\) có: \(\widehat {DA{\rm{E}}} = \widehat {AD{\rm{M}}} = \widehat {A{\rm{EM}}} = {90^0}\left( {giả \,\, thiết} \right)\)
\(\Rightarrow \) Tứ giác \(ADME\) là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
Vì \(O\) là trung điểm của đường chéo \(DE\) (giả thiết)
\(\Rightarrow \) \(O\) cũng là trung điểm của \(AM\) (tính chất hình chữ nhật)
Vậy \(A, O, M\) thẳng hàng.
b) Kẻ \(AH ⊥ BC\), kẻ \(OK ⊥ BC\)
Cách 1:
Ta có \(OA = OM\) (do \(O\) là trung điểm của \(AM\))
\(OK // AH\) (do cùng vuông góc với \(BC\)).
\(\Rightarrow \) \(K\) là trung điểm của \(MH\) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)
\(\Rightarrow \) \(OK =\dfrac{1}{2}AH\) (tính chất đường trung bình của tam giác)
Điểm \(O\) cách đoạn \(BC\) cố định một khoảng không đổi bằng \(\dfrac{1}{2}AH\).
Mặt khác khi \(M\) trùng \(C\) thì \(O\) chính là trung điểm của \(AC\), khi \(M\) trùng \(B\) thì \(O\) chính là trung điểm của \(AB\).
Vậy \(O\) di chuyển trên đoạn thẳng \(PQ\) là đường trung bình của \(\Delta ABC\).
Cách 2:
Vì \(O\) là trung điểm của \(AM\) nên \(HO\) là trung tuyến ứng với cạnh huyền \(AM\). Do đó \(OA = OH\). Suy ra điểm \(O\) di chuyển trên đường trung trực của \(AH\).
Mặt khác vì \(M\) di chuyển trên đoạn \(BC\). Vậy điểm \(O\) di chuyển trên đoạn thẳng \(PQ\) là đường trung bình của \(ABC\).
c) Ta có \(AH\) là đường cao hạ từ \(A\) đến \(BC\) do đó \(AM\ge AH\) (trong tam giác vuông, cạnh huyền là cạnh lớn nhất).
Vậy \(AM\) nhỏ nhất bằng \(AH\) khi \(M\) trùng \(H\).
soanvan.me