Video hướng dẫn giải
Một hình trụ có hai đáy là hai hình tròn \((O;r)\) và \((O';r)\). Khoảng cách giữa hai đáy là \(OO' = r.\sqrt3\). Một hình nón có đỉnh là \(O'\) và có đáy là hình tròn \((O;r)\).
LG a
a) Gọi \(S_1\) là diện tích xung quanh của hình trụ và \(S_2\) là diện tích xung quanh của hình nón, hãy tính tỷ số \({{{S_1}} \over {{S_2}}}\).
Phương pháp giải:
+) Diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi Rh\) với \(R;h\) lần lượt là bán kính đáy và chiều cao của hình trụ.
+) Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\) với \(r;l\) lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
Lời giải chi tiết:
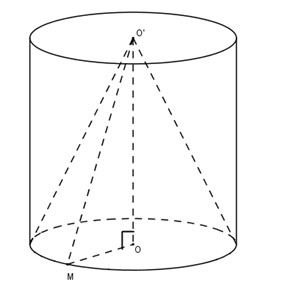
Hình trụ có chiều cao \(l = h = r\sqrt3\) và bán kính đáy \(r\) nên diện tích xung quanh hình trụ là:
\[S_1 = 2πr.h = 2πr.r\sqrt3 = 2\sqrt3 πr^2\]
Với \(M\) là một điểm bất kì thuộc đường tròn \((O)\) thì \(O'M\) là một đường sinh của hình nón ta có:
\(l' = O'M = \sqrt {OO{'^2} + O{M^2}} = \sqrt {3{r^2} + {r^2}} = 2r\)
Hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l=2r\) nên diện tích xung quanh hình nón là:
\[S_2 = πrl'= π.r.2r = 2πr^2\]
Vậy: \({{{S_1}} \over {{S_2}}} = {{2\sqrt 3 \pi {r^2}} \over {2\pi {r^2}}} = \sqrt 3 \)
LG b
b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỷ số thể tích hai phần đó.
Phương pháp giải:
Mặt xung quanh của hình nón chia khối trụ thành hai phần: Phần dưới là khối nón và phần còn lại.
+) Tính thế tích của khối nón: \({V_1} = \dfrac{1}{3}\pi {r^2}h\) và thể tích của hình trụ: \(V = \pi {r^2}h\)
+) Suy ra thể tích phần còn lại: \({V_2} = V - {V_1}\).
+) Tính tỉ số: \(\dfrac{{{V_1}}}{{{V_2}}}\)
Lời giải chi tiết:
Mặt xung quanh của hình nón chia khối trụ thành hai phần: Phần dưới là khối nón và phần còn lại.
Gọi V là thể tích khối trụ ta có: \(V = \pi {r^2}h\)
Gọi \(V_1\) là thể tích khối nón ta có: \({V_1} = \dfrac{1}{3}\pi {r^2}h\)
Gọi \(V_2\) là thế tích phần còn lại ta có: \({V_2} = V - {V_1} = \pi {r^2}h - \dfrac{1}{3}\pi {r^2}h = \dfrac{2}{3}\pi {r^2}h\)
Vậy tỉ số \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{1}{3}\pi {r^2}h}}{{\dfrac{2}{3}\pi {r^2}h}} = \dfrac{1}{2}\).
Cách khác:
Tính trực tiếp như sau:
Thể tích khối trụ là:
\({V_{\text{trụ}}} = \pi {r^2}h = \pi {r^2}.r\sqrt 3 = \pi {r^3}\sqrt 3 \)
Thể tích khối nón là:
\({V_{\text{nón}}} = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {r^2}.r\sqrt 3 = \frac{{\pi {r^3}\sqrt 3 }}{3}\)
Thể tích của khối trụ nằm ngoài khối nón là:
\(V = {V_{\text{trụ}}} - {V_{\text{nón}}} = \pi {r^3}\sqrt 3 - \frac{{\pi {r^3}\sqrt 3 }}{3} = \frac{{2\sqrt 3 }}{3}\pi {r^3}\)
Mặt xung quanh của hình nón chia khối tru thành hai phần, tỉ số thể tích hai phần đó là:
\(\frac{V}{{{V_{\text {nón}}}}} = \frac{{2\sqrt 3 }}{3}\pi {r^3}:\frac{{\pi {r^3}\sqrt 3 }}{3} = 2\)
soanvan.me
