Đề bài
Xác định hệ số \(a\) của hàm số \(y=ax^2\), biết rằng đồ thị của nó đi qua điểm \(A(-2; 1).\) Vẽ đồ thị của hàm số đó.
Phương pháp giải - Xem chi tiết
+) Thay tọa độ điểm \(A\left( { - 2;1} \right)\) vào hàm số \(y = a{x^2}\) để tìm \(a.\)
+) Xác định một số điểm thuộc đồ thị \(y = a{x^2}\) vừa tìm được và vẽ parabol đi qua các điểm đó.
Lời giải chi tiết
+) Thay \(x = - 2;y = 1\) vào hàm số \(y = a{x^2}\) ta được \(1 = a.{\left( { - 2} \right)^2} \)\(\Rightarrow a = \dfrac{1}{4}\)
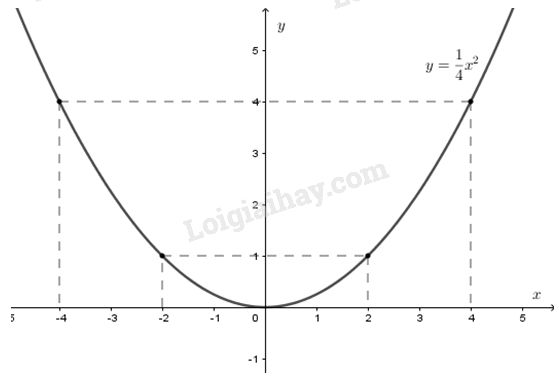
Hàm số là \(y = \dfrac{1}{4}{x^2}.\)
Đồ thị hàm số \(y = \dfrac{1}{4}{x^2}.\) (hình vẽ)
+) Ta có bảng sau:
| \(x\) | \( - 4\) | \(-3\) | \( - 2\) | \(0\) | \(2\) | \(3\) | \(4\) |
| \(y = \dfrac{1}{4}{x^2}\) | \(4\) | \(\dfrac{9}{4}\) | \(1\) | \(0\) | \(1\) | \(\dfrac{9}{4}\) | \(4\) |
soanvan.me
