Một hình chữ nhật có kích thước là \(25cm\) và \(40cm\). Người ta tăng mỗi kích thước của hình chữ nhật thêm \(x\) cm. Gọi \(S\) và \(P\) thứ tự là diện tích và chu vi của hình chữ nhật mới tính theo \(x\).
LG câu a
Hỏi các đại lượng \(S\) và \(P\) có phải là hàm số bậc nhất của \(x\) không ? Vì sao ?
Phương pháp giải:
Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\), trong đó \(a,b\) là các số cho trước và \(a \ne 0\).
Lời giải chi tiết:
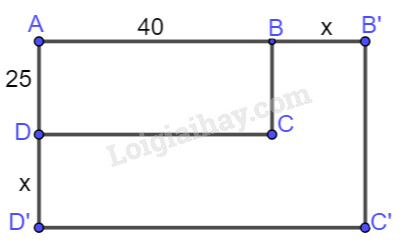
Sau khi tăng kích thước của mỗi chiều, ta được hình chữ nhật \(AB’C’D’\) có chiều dài \(AB’=\left( {40 + x} \right)\) cm, chiều rộng \(AD'=\left( {25 + x} \right)\) cm.
Diện tích hình chữ nhật mới :
\(S = \left( {40 + x} \right)\left( {25 + x} \right)\)\( =1000+40x+25x+x^2\)\(= 1000 + 65x + {x^2}\)
S không phải là hàm số bậc nhất đối với \(x\) vì có bậc của biến số \(x\) là bậc hai.
Chu vi hình chữ nhật mới:
\(P = 2.\left[ {\left( {40 + x} \right) + \left( {25 + x} \right)} \right]\)\( =2(2x+65)= 4x + 130\)
P là hàm số bậc nhất đối với x có hệ số \(a = 4\), hệ số \(b = 130.\)
LG câu b
Tính các giá trị tương ứng của \(P\) khi \(x\) nhận các giá trị ( tính theo đơn vị cm) sau:
0; 1; 1,5; 2,5; 3,5.
Phương pháp giải:
Tính \(f({x_0})\) bằng cách thay \(x = {x_0}\) vào \(f(x)\).
Lời giải chi tiết:
Các giá trị tương ứng của \(P\) là:
|
\(x\) |
0 |
1 |
1,5 |
2,5 |
3,5 |
|
\(P=4x+130\) |
130 |
134 |
136 |
140 |
144 |
soanvan.me
