Đề bài
Cho hai tam giác ABC và MNP có \(\widehat {ACB} = \widehat {MPN}\), \(\widehat {ACB} = \widehat {MPN}\). Cần thêm một điều kiện để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc – cạnh – góc là:
A. AC = MP;
B. AB = MN;
C. BC = NP;
D. AC = MN.
Phương pháp giải - Xem chi tiết
Xét các điều kiện để hai tam giác ABC và MNP bằng nhau theo trường hợp góc – cạnh – góc.
Lời giải chi tiết
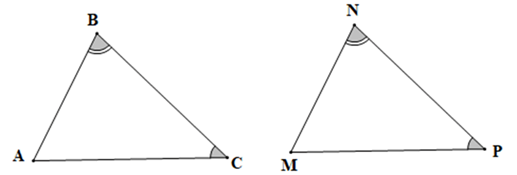
Để ΔABC = ∆MNP theo trường hợp góc – cạnh – góc thì hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.
Mà \(\widehat {ABC} = \widehat {MNP},\widehat {ACB} = \widehat {MPN}\)
Lại có \(\widehat {ABC}\) và \(\widehat {ACB}\) là hai góc kề cạnh BC;
\(\widehat {MNP}\) và \(\widehat {MPN}\) là hai góc kề cạnh NP.
Do đó điều kiện còn thiếu là điều kiện về cạnh, đó là BC = NP.
Vậy ta chọn đáp án C.
