Đề bài
Các cặp tam giác trong mỗi hình 41a, b, c, d, e có bằng nhau không ? Nếu có, chúng bằng nhau theo trường hợp nào ?
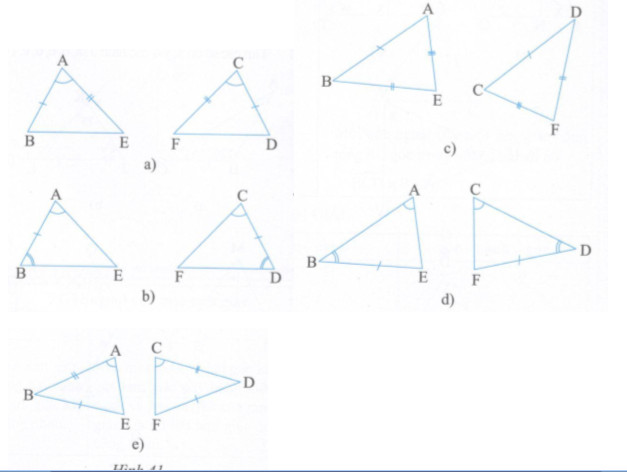
Lời giải chi tiết
\(\eqalign{ & a)\Delta ABE = \Delta CDF(c.g.c) \cr & b)\Delta ABE = \Delta CDF(g.c.g) \cr & c)\Delta ABE = \Delta CDF(c.c.c) \cr & d) Vì \widehat {A}+\widehat {B}+\widehat {E}= 180^{0} \cr & \widehat {C}+\widehat {D}+\widehat {F}= 180^{0} \cr & nên \widehat {B}=\widehat {D} \cr & Xét \Delta AEB = \Delta CFD có \cr &\widehat {B}=\widehat {D} \cr & \widehat {E}=\widehat {F} \cr & BE=DF \cr & Nên \Delta AEB = \Delta CFD (g-c-g) \cr }\)
e) Kẻ \( BH \bot AE, DK \bot CF \), ta được
+) \(\Delta ABH =\Delta CDK \)( cạnh huyền - góc nhọn)
nên \(BH=DK; AH=CK \) ( 2 cạnh tương ứng)
+) \(\Delta HBE =\Delta KDF \)(cạnh huyền- cạnh góc vuông)
nên EH=KF ( 2 cạnh tương ứng)
Ta có: \(AE=AH+HE; CF=CK+KF \) nên \(AE=CF\)
suy ra\(\Delta ABE =\Delta CDF \) (c-c-c)
soanvan.me
