Đề bài
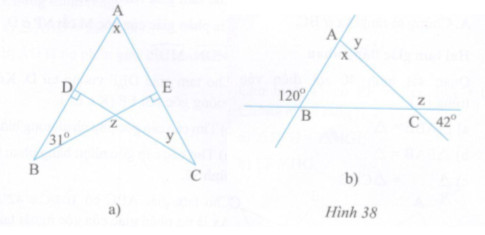
Tìm số đo x, y, z ở các hình 38a, b:
Lời giải chi tiết
a)Tam giác AEB vuông tại E có: \(\widehat {EAB} = \widehat {EBA} = {90^0}\)
Do đó: \(x + {31^0} = {90^0} \Rightarrow x = {90^0} - {31^0} = {59^0}\)
Tam giác ADC vuông tại D có:
\(\widehat {DAC} + \widehat {ACD} = {90^0} \Leftrightarrow x + y = {90^0} \Rightarrow y = {90^0} - {59^0} = {31^0}\)
\(z = \widehat {BEC} + \widehat {ECD}\) (góc ngoài của tam giác) \( \Rightarrow z = {90^0} + {31^0} = {121^0}\)
b) \(\widehat {ACB} = {42^0}\) (hai góc đối đỉnh)
\({120^0} + \widehat {ABC} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {ABC} = {180^0} - {120^0} = {60^0}\)
Tam giác ABC có: \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = {180^0} \Rightarrow {60^0} + {42^0} + \widehat {BAC} = {180^0}\)
\( \Rightarrow \widehat {BAC} = {180^0} - {60^0} - {42^0} = {78^0} \Rightarrow x = {78^0}\)
\(y + x = {180^0}\) (hai góc kề bù) \( \Rightarrow y = {180^0} - {78^0} = {102^0}\)
\(z + \widehat {ACB} = {180^0}\) (hai góc kề bù) \( \Rightarrow z = {180^0} - {42^0} = {138^0}\)
soanvan.me
