Đề bài
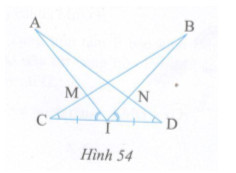
Ở hình 54 cho biết \(\widehat {MCI} = \widehat {NDI},\,\,\widehat {MIC} = \widehat {NID},\,\,IC = ID.\) Chứng minh rằng:
\(\eqalign{ & a)\,\,\Delta MCI = \Delta NDI \cr & b)AD = BC \cr & c)AM = BN \cr} \)
Lời giải chi tiết
a)Xét tam giác MCI và NDI ta có: \(\eqalign{ & \widehat {MCI} = \widehat {NDI}(gt) \cr & CI = DI(gt) \cr & \widehat {MIC} = \widehat {NID}(gt) \cr} \)
Do đó: \(\Delta MCI = \Delta NDI(c.g.c)\)
b) Ta có: \(\widehat {CIB} = \widehat {CIM} + \widehat {AIB}\) và \(\widehat {AID} = \widehat {AIB} + \widehat {NID}\)
Mà \(\widehat {CIM} = \widehat {NID}\) (giả thiết) nên \(\widehat {CIB} = \widehat {AID}\)
Xét tam giác CIB và AID có: \(\eqalign{ & \widehat {ICB} = \widehat {IDA}(gt) \cr & CI = DI(gt) \cr & \widehat {CIB} = \widehat {DIA}(cmt) \cr} \)
Do đó: \(\Delta CIB = \Delta DIA(g.c.g) \Rightarrow BC = AD\)
c) Ta có: \(\Delta MCI = \Delta NDI\) (chứng minh câu a) => MI = NI
AM + MI = AI và BN + NI = BI
Mà MI = NI và AI = BI \((\Delta CIB = \Delta DIA)\) nên AM = BN.
soanvan.me
