Đề bài
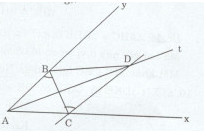
Cho góc xAy nhọn có At là tia phân giác. Trên tia At ta lấy điểm D, đường thẳng song song với Ay kẻ từ D cắt Ax tại C.
a) Chứng minh rằng \(\widehat {CAD} = \widehat {CDA}\)
b) Trên Ay, lấy điểm B sao cho AB = AC. Chứng minh rằng \(\Delta ACD = \Delta ABD\)
c) Chứng minh rằng AC = DB và AC // DB.
Lời giải chi tiết
a)Ay // DC (gt)\( \Rightarrow \widehat {yAD} = \widehat {ADC}\) (hai góc so le trong).
Mà \(\widehat {yAD} = \widehat {CAD}\) (At là tia phân giác góc xAy)
Do đó: \(\widehat {CAD} = \widehat {ADC}\)
b) Xét tam giác ACD và ABD có:
AC = AB (gt)
\(\widehat {CAD} = \widehat {BAD}\) (At là tia phân giác của góc xAy)
AD là cạnh chung.
Do đó: \(\Delta ACD = \Delta ABD(c.g.c)\)
c) \(Ay//CD \Rightarrow \widehat {ABC} = \widehat {DCB}\) (hai góc so le trong)
\(\Delta ACD = \Delta ABD\) (chứng minh câu b) \( \Rightarrow \widehat {ACD} = \widehat {ABD}\)
Mà \(\widehat {DBC} + \widehat {ABC} = \widehat {ABD};\widehat {ACB} + \widehat {BCD} = \widehat {ACD}.\) Nên \(\widehat {DBC} = \widehat {ACB}\)
Xét tam giác ABC và DCB có:
\(\eqalign{ & \widehat {ABC} = \widehat {DCB}(cmt) \cr & \widehat {ACB} = \widehat {DBC}(cmt) \cr} \)
BC là cạnh chung.
Do đó: \(\Delta ABC = \Delta DCB(g.c.g) \Rightarrow AC = BD\)
Ta có: \(\widehat {DBC} = \widehat {BCA}\) (chứng minh trên)
Mà hai góc này ở vị trí so le trong nên BD // AC.
soanvan.me
