Đề bài
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 40 cm, cạnh bên SA = 48 cm.
a) Tính chiều cao và thể tích của hình chóp.
b) Tính trung đoạn và diện tích toàn phần của hình chóp.
Lời giải chi tiết
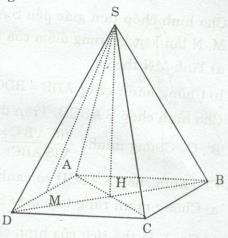
a) ABCD là đa giác đều => ABCD là hình vuông
∆ABC vuông tại B có:
\(A{C^2} = A{B^2} + B{C^2}\) (định lí Py-ta-go)
\(\eqalign{ & \Rightarrow A{C^2} = {6^2} + {6^2} = 72 \cr&\Rightarrow AC = 6\sqrt 2 (cm) \cr & \Rightarrow AH = {{6\sqrt 2 } \over 2} = 3\sqrt 2 (cm) \cr} \)
∆SAH vuông tại H có:
\(S{H^2} + A{H^2} = S{A^2}\) (định lí Py-ta-go)
\(\eqalign{ & \Rightarrow S{H^2} + 18 = {48^2} \cr & \Rightarrow S{H^2} = 2286 \Rightarrow SH = 3\sqrt {254} (cm) \cr} \)
Thể tích của hình chóp: \(V = {1 \over 3}{S_d}.h = {1 \over 3}{.40^2}.3\sqrt {254}\)\(\, = 1600\sqrt {254} (c{m^3})\)
b) ∆SAD cân tại S có SM là đường trung tuyến
=> SM là đường cao \( \Rightarrow SM \bot AD\) tại M
Trung đoạn của hình chóp: \(d = SM = \sqrt {S{A^2} - A{M^2}} \)\(\, = \sqrt {{{48}^2} - {{20}^2}} = 4\sqrt {119} (cm)\)
Diện tích xung quanh của hình chóp:
\({S_{xq}} = p.d = 2AB.SM = 2.40.4\sqrt {119} \)\(\,= 320\sqrt {119} (c{m^2})\)
Diện tích toàn phần của hình chóp: \({S_{tp}} = {S_{xq}} + {S_d} \)\(\,= 320\sqrt {119} + {40^2} \approx 5090,79(c{m^2})\)
soanvan.me
