Đề bài
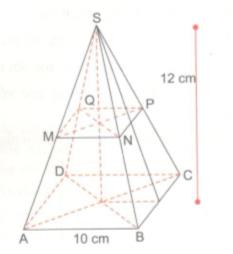
Cho hình chóp tứ giác đều S.ABCD với kích thước đã ghi trên hình. Gọi M, N, P, Q lần lượt là các trung điểm các cạnh bên.
a) Tính thể tích các khối chóp A.ABCD và S.MNPQ.
b) Tính thể tích khối chóp cụt MNPQ.ABCD.
Lời giải chi tiết
a) Thể tích khối chóp S.ABCD: \({V_1} = {1 \over 3}.{S_{ABCD}}.SH = {1 \over 3}{.10^2}.12\)\(\, = 400(c{m^3})\)
(với H là giao điểm của AC và DB)
Gọi K là giao điểm của MP và QN => SK là đường cao của khối chóp S.MNPQ
M, P lần lượt là trung điểm của SA và SC (gt)
=> MP là đường trung bình của tam giác SAC
\( \Rightarrow MP//AC \Rightarrow MK//AH(K \in MP,H \in AC)\)
∆SAH có MK // AH và M là trung điểm của SA (gt)
=> K là trung điểm của SH \( \Rightarrow SK = {{SH} \over 2} = 6(cm)\)
Thế tích khối chóp S.MNPQ:
\({V_2} = {1 \over 3}.{S_{MNPQ}}.SK = {1 \over 3}.M{N^2}.SK \)
\(\;\;\;\;\;= {1 \over 3}{\left( {{{AB} \over 2}} \right)^2}.SK = {1 \over 3}{.5^2}.6 = 50(c{m^3})\)
b) Thể tích khối chóp cụt đều MNPQ.ABCD:
Vcụt đều = V1 – V2 = 400 -50 = 350 (cm3)
soanvan.me
