LG a
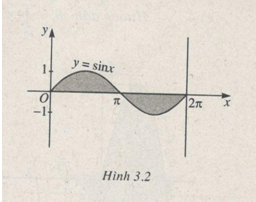
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sin x\), trục hoành, trục tung và đường thẳng \(x = 2\pi \)
Lời giải chi tiết:
Ta có \(\sin x \ge 0\) trên đoạn \(\left[ {0 ;\pi } \right]\) và \(\sin x \le 0\) trên đoạn \(\left[ {\pi ;2\pi } \right]\).
Vậy diện tích hình phẳng (phần tô đậm trong hình 3.2) là:
\(S = \int\limits_0^{2\pi } {\left| {\sin x} \right|dx = \int\limits_0^\pi {\sin xdx - } } \int\limits_\pi ^{2\pi } {\sin xdx} \)
\(= 2 - \left( { - 2} \right) = 4\)
LG b
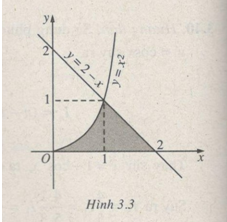
Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = 2 - x,y = {x^2}\) và trục hoành trong miền \(x \ge 0\)
Lời giải chi tiết:
Tìm hoành độ giao điểm của hai đồ thị hàm số \(y = 2 - x\) và \(y = {x^2}\) bằng cách giải phương trình \(2 - x = {x^2}\). Ta tìm được \(x = 1\) và \(x = - 2\) (loại). Hình tạo thành (phần tô đậm trong hình 3.2) gồm một tam giác cong và một tam giác. Diện tích tam giác cong là:\(\int\limits_0^1 {{x^2}dx} = {1 \over 3}\). Diện tích tam giác là \({1 \over 2}\).
Vậy diện tích hình phẳng cần tìm là: \({1 \over 3} + {1 \over 2} = {5 \over 6}\)
soanvan.me
