Video hướng dẫn giải
Nhắc lại định nghĩa:
LG a
Góc giữa đường thẳng và mặt phẳng.
Phương pháp giải:
Xem lại lý thuyết bài Đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:
Góc giữa đường thẳng và mặt phẳng
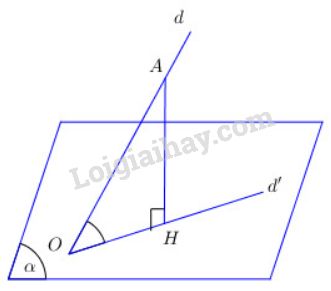
Định nghĩa: Cho đường thẳng \(d\) và mặt phẳng \((\alpha)\).
Trường hợp đường thẳng \(d\) vuông góc với mặt phẳng \((\alpha)\) thì ta nói rằng góc giữa đường thẳng \(d\) và mặt phẳng \((\alpha)\) bằng \(90^0\).
Trường hợp đường thẳng \(d\) không vuông góc với mặt phẳng \((\alpha)\) thì góc giữa \(d\) và hình chiếu \(d'\) của nó trên \(\alpha\) gọi là góc giữa đường thẳng \(d\) và mặt phẳng \((\alpha)\).
- Nếu \(d \, //\left( \alpha \right)\) hoặc \(d \subset \left( \alpha \right)\) thì góc giữa \(d\) và mặt phẳng \((\alpha)\) bằng \(0^0\).
LG b
Góc giữa hai mặt phẳng.
Phương pháp giải:
Xem lại lý thuyết bài Hai mặt phẳng vuông góc.
Lời giải chi tiết:
Góc giữa hai mặt phẳng
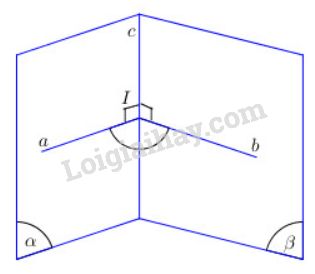
Định nghĩa: Giả sử hai mặt phẳng \((α)\) và \((β)\) cắt nhau theo giao tuyến \(c\). Từ điểm \(I\) bất kì trên \(c\), trong mặt phẳng \((α)\) ta dựng đường thẳng \(a\) vuông góc với \(c\) và trong mặt phẳng \((β)\) ta dựng đường thẳng \(b\) vuông góc với \(c\). Ta gọi góc giữa hai đường thẳng \(a\) và \(b\) là góc giữa hai mặt phẳng \((α)\) và \((β)\).
Nếu \(\left( \alpha \right)//\left( \beta \right)\) hoặc \(\left( \alpha \right)\equiv \left( \beta \right)\) thì góc giữa hai mặt phẳng bằng \(0^0\).
Chú ý: góc giữa hai mặt phẳng luôn luôn nhỏ hơn hoặc bằng \(90^0\).
soanvan.me
