Video hướng dẫn giải
Hãy nêu cách tính khoảng cách:
LG a
Từ một điểm đến một đường thẳng
Phương pháp giải:
Xem lại lý thuyết bài Khoảng cách.
Lời giải chi tiết:
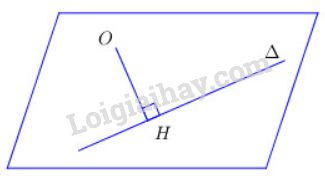
Để tính khoảng cách từ điểm \(O\) đến đường thẳng \(Δ\) không đi qua \(O\), ta xác định mặt phẳng \((O,Δ)\) và trong mặt phẳng này kẻ \(OH ⊥ Δ\). Khi đó độ dài \(OH\) chính là khoảng cách từ \(O\) đến \(Δ\).
LG b
Từ đường thẳng \(a\) đến mặt phẳng \((α)\) song song với \(a\)
Phương pháp giải:
Xem lại lý thuyết bài Khoảng cách.
Lời giải chi tiết:
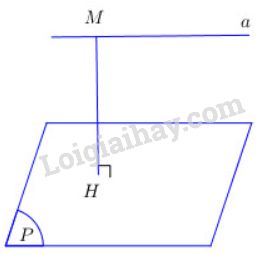
Để tính khoảng cách giữa đường thẳng \(a\) và mp \((P)\) song song với \(a\), ta lấy một điểm \(M\) bất kì thuộc đường thẳng \(a\). Khoảng cách \(MH\) từ điểm \(M\) đến mp \((P)\) chính là khoảng cách giữa đường thẳng \(a\) với mp \((P)\) song song với \(a\).
LG c
Giữa hai mặt phẳng song song
Phương pháp giải:
Xem lại lý thuyết bài Khoảng cách.
Lời giải chi tiết:
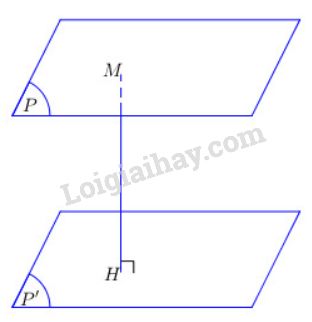
Để tìm khoảng cách giữa hai mp \((P)\) và \((P’)\) song song với nhau, ta lấy một điểm \(M\) thuộc \((P)\) và tìm khoảng cách \(MH\) từ điểm \(M\) đến mặt phẳng \((P’)\)
soanvan.me
