Cho hàm số \(y = f(x) = 2\sin 2x\)
a. Chứng minh rằng với số nguyên \(k\) tùy ý, luôn có \(f(x + kπ) = f(x)\) với mọi \(x\).
b. Lập bảng biến thiên của hàm số \(y = 2\sin 2x\) trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
c. Vẽ đồ thị của hàm số \(y = 2\sin 2x\).
LG a
Chứng minh rằng với số nguyên \(k\) tùy ý, luôn có \(f(x + kπ) = f(x)\) với mọi \(x\).
Lời giải chi tiết:
Ta có \(f(x + kπ) = 2\sin 2(x + kπ) \)
\(= 2\sin (2x + k2π) = 2\sin 2x = f(x),\) \( ∀ x \in\mathbb R\)
LG b
Lập bảng biến thiên của hàm số \(y = 2\sin 2x\) trên đoạn \(\left[ { - {\pi \over 2};{\pi \over 2}} \right].\)
Lời giải chi tiết:
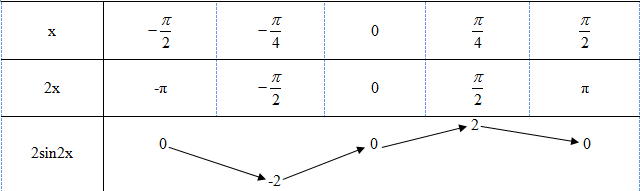
Bảng biến thiên :
LG c
Vẽ đồ thị của hàm số \(y = 2\sin 2x\).
Lời giải chi tiết:
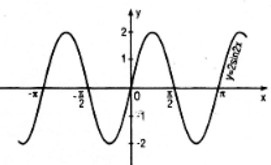
Đồ thị :
soanvan.me
