Đề bài
Người ta có thể sản xuất amoniac để điều chế ure bằng cách chuyển hóa có xúc tác một hỗn hợp không khí, hơi nước và khí metan (thành phần chính của khí thiên nhiên).
Phản ứng điều chế \({H_2}\) và \(C{O_2}\) : \(C{H_4} + 2{H_2}O \to C{O_2} + 4{H_2}\) (1)
Phản ứng thu \({N_2}\) (từ không khí) và \(C{O_2}\): \(C{H_4} + 2{O_2} \to C{O_2} + 2{H_2}O\) (2)
Phản ứng tổng hợp \(N{H_3}\) :
![]()
Để sản xuất khí amoniac, nếu lấy 841,7 \({m^3}\)không khí (chứa 21,03% \({O_2}\), 78,02 \({N_2}\), còn lại là khí hiếm), thì cần phải lấy bao nhiêu \({m^3}\) khí metan và bao nhiêu \({m^3}\) hơi nước để có đủ lượng \({N_2}\) và \({H_2}\) theo tỉ lệ 1:3 về thể tích dùng cho phản ứng tổng hợp amoniac. Giả thiết các phản ứng (1) và (2) đều xảy ra hoàn thành và các thể tích khi được đo ở cùng điều kiện.
Lời giải chi tiết
Thể tích khí \({O_2}\) và khí \({N_2}\) trong 841,7 \({m^3}\) không khí:
\({V_{{O_2}}} = \frac{{841,7.21,03}}{{100}} = 177,01({m^3});\)
\({V_{{N_2}}} = \frac{{841,7.78,02}}{{100}} = 656,69({m^3})\)
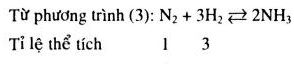
\({V_{{H_2}}}\)cần = \(3.{V_{{N_2}}} = 3.656,69 = 1970,08({m^3})\)
Từ phương trình (1): \(C{H_4} + 2{H_2}O \to C{O_2} + 4{H_2}\)
\(1{m^3} \to 2{m^3} \to 1{m^3} \to 4{m^3}\)
? \( \leftarrow \) ? \( \leftarrow \) 1970,08 \({m^3}\)
\({V_{C{H_4}}} = \frac{{1970,08}}{4} = 492,52({m^3})\)
\({V_{{H_2}O}} = 2.492,52 = 985,04({m^3})\)
Từ phương trình (2): \(C{H_4} + 2{O_2} \to C{O_2} + 2{H_2}O\)
\(1{m^3} \to 2{m^3}\)
? \( \leftarrow \)177,01 \({m^3}\) \( \to \) 177,01 \({m^3}\)
\({V_{C{H_4}}} = \frac{{177,01}}{2} = 88,5({m^3})\)
Vậy thể tích \(C{H_4}\) và \({H_2}\) tổng cộng cần:
\({V_{C{H_4}}} = 492,52 + 88m5 = 581,02({m^3});\)
\({V_{{H_2}O}} = 985,04 - 177,01 = 808,03({m^3})\)
soanvan.me
