Câu hỏi khởi động
Chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau, lấy ra hình vuông nhỏ thứ nhất (ở góc dưới bên trái, màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{2}.\)
Chia hình vuông nhỏ ở góc trên bên phải thành bốn hình vuông bằng nhau, lấy ra hình vuông nhỏ thứ hai (màu đỏ), cạnh của hình vuông đó bằng \(\frac{1}{4}.\)
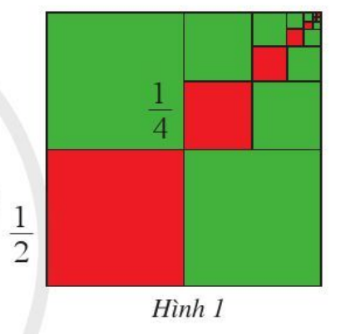
Tiếp tục quá trình trên ta được dãy các hình vuông nhỏ (màu đỏ) ở hình 1.
Cạnh của hình vuông nhỏ thứ n (màu đỏ) bằng bao nhiêu? Vì sao?
Lời giải chi tiết:
Nhận xét:
Chia hình vuông cạnh a thành 4 hình vuông, lấy ra hình vuông nhỏ thứ nhất (như cách lấy ở trên) thì cạnh của hình vuông đó bằng \(\frac{a}{2}\).
=> Sau mỗi lần lấy, độ lớn của cạnh hình vuông giảm đi 2 lần
=> Sau n lần, cạnh hình vuông nhỏ thứ n giảm đi \({2^n}\) so với hình ban đầu.
=> Cạnh của hình vuông nhỏ thứ n là \(\frac{1}{{{2^n}}}\)
Hoạt động
Xét mệnh đề chứa biến P(n): “\(1 + 3 + 5 + ... + (2n - 1) = {n^2}\)” với n là số nguyên dương.
a) Chứng tỏ rằng P(1) là mệnh đề đúng.
b) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, cho biết \(1 + 3 + 5 + ... + (2k - 1)\) bằng bao nhiêu.
c) Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, chứng tỏ rằng P(k+1) cũng là mệnh đề đúng bằng cách chỉ ra \({k^2} + [2(k + 1) - 1] = {(k + 1)^2}\).
Lời giải chi tiết:
a) Mệnh đề P(1) là: “\(1 = {1^2}\)”, rõ ràng mệnh đề này đúng.
b) Mệnh đề P(k) là: “\(1 + 3 + 5 + ... + (2k - 1) = {k^2}\)”
Mệnh đề P(k) đúng thì \(1 + 3 + 5 + ... + (2k - 1)\) bằng \({k^2}\)
c) Mệnh đề P(k+1) là: “\(1 + 3 + 5 + ... + [2(k + 1) - 1] = {(k + 1)^2}\)”
Mệnh đề P(k) đúng nên ta có \(1 + 3 + 5 + ... + (2k - 1) = {k^2}\)
\(\begin{array}{l} \Rightarrow 1 + 3 + 5 + ... + [2(k + 1) - 1] = 1 + 3 + 5 + ... + (2k - 1) + [2(k + 1) - 1]\\ = {k^2} + [2(k + 1) - 1] = {k^2} + 2k + 1 = {(k + 1)^2}\end{array}\)
Vậy mệnh đề P(k+1) cũng đúng.
Luyện tập – vận dụng 1
Chứng minh:
a) \(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt n + \sqrt {n + 1} }} = \sqrt {n + 1} - 1\) với mọi \(n \in \mathbb{N}*\)
b) \(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)
Phương pháp giải:
Chứng minh mệnh đề P(n) đúng với \(n \ge p\) thì:
Bước 1: Chứng tỏ mệnh đề đúng với \(n = p\)
Bước 2: Với k là một số nguyên dương tùy ý mà P(k) là mệnh đề đúng, ta chứng tỏ P(k+1) cũng là mệnh đề đúng.
Lời giải chi tiết:
a) Ta chứng minh bằng quy nạp theo n.
Bước 1: Khi \(n = 1\) ta có \(\frac{1}{{\sqrt 1 + \sqrt 2 }} = \sqrt 2 - 1\), đúng
vì \(\left( {\sqrt 2 + \sqrt 1 } \right)\left( {\sqrt 2 - \sqrt 1 } \right) = 2 - 1 = 1 \Rightarrow \frac{1}{{\sqrt 2 + \sqrt 1 }} = \sqrt 2 - \sqrt 1 = \sqrt 2 - 1\)
Như vậy đẳng thức đúng với \(n = 1\)
Bước 2: Với k là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }} = \sqrt {k + 2} - 1\)
Thật vậy, theo giả thiết quy nạp ta có:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt k + \sqrt {k + 1} }} = \sqrt {k + 1} - 1\)
Suy ra
\(\begin{array}{l}\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }}\\ = \sqrt {k + 1} - 1 + \frac{1}{{\sqrt {k + 1} + \sqrt {k + 2} }}\\ = \frac{{{{\left( {\sqrt {k + 1} } \right)}^2} + \sqrt {k + 1} .\sqrt {k + 2} + 1}}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \frac{{k + 2 + \sqrt {k + 1} .\sqrt {k + 2} }}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \frac{{\sqrt {k + 2} \left( {\sqrt {k + 2} + \sqrt {k + 1} } \right)}}{{\sqrt {k + 1} + \sqrt {k + 2} }} - 1\\ = \sqrt {k + 2} - 1\end{array}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*\). Tức là:
\(\frac{1}{{\sqrt 1 + \sqrt 2 }} + \frac{1}{{\sqrt 2 + \sqrt 3 }} + ... + \frac{1}{{\sqrt n + \sqrt {n + 1} }} = \sqrt {n + 1} - 1\) với mọi \(n \in \mathbb{N}*\)
b) Ta chứng minh bằng quy nạp theo n.
Bước 1: Khi \(n = 2\) ta có \(\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}}\), đúng
vì \(\frac{{{2^3} - 1}}{{{2^3} + 1}} = \frac{7}{9};\frac{{2({2^2} + 2 + 1)}}{{3.2(2 + 1)}} = \frac{{2.7}}{{3.2.3}} = \frac{7}{9}\)
Như vậy đẳng thức đúng với \(n = 2\)
Bước 2: Với k là một số nguyên dương lớn hơn 2 tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức đúng với k+1, tức là:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)
Thật vậy, theo giả thiết quy nạp ta có:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}} = \frac{{2({{(k + 1)}^2} + (k + 1) + 1)}}{{3(k + 1)(k + 2)}}\)
Suy ra
\(\begin{array}{l}\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{{{(k + 1)}^3} - 1}}{{{{(k + 1)}^3} + 1}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{[(k + 1) - 1][{{(k + 1)}^2} + (k + 1) + 1]}}{{[(k + 1) + 1][{{(k + 1)}^2} - (k + 1) + 1]}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + 2k + 1 - k - 1 + 1)}}\\ = \frac{{2({k^2} + k + 1)}}{{3k(k + 1)}}.\frac{{k[{{(k + 1)}^2} + (k + 1) + 1]}}{{(k + 2)({k^2} + k + 1)}}\\ = \frac{{2[{{(k + 1)}^2} + (k + 1) + 1]}}{{3(k + 1)(k + 2)}}\end{array}\)
Vậy đẳng thức đúng với k+1. Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in \mathbb{N}*,n \ge 2\). Tức là:
\(\frac{{{2^3} - 1}}{{{2^3} + 1}}.\frac{{{3^3} - 1}}{{{3^3} + 1}}.\frac{{{4^3} - 1}}{{{4^3} + 1}}...\frac{{{n^3} - 1}}{{{n^3} + 1}} = \frac{{2({n^2} + n + 1)}}{{3n(n + 1)}}\) với mọi \(n \in \mathbb{N}*,n \ge 2\)
