HĐ7
Viết tập hợp X gồm những thành viên tham gia cả hai chuyên đề 1 và 2 trong tình huống mở đầu.
Tập X có phải là tập con của tập A không? Tập X có phải là tập con của tập B không? (A, B là các tập hợp trong HĐ1).
Lời giải chi tiết:

X = {Khánh; Bình; Hương; Chi; Tú}
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Dễ thấy: Các phần tử của X đều là phần tử của tập hợp A và tập hợp B.
Do đó \(X \subset A\) và \(X \subset B\).
Luyện tập 5
Cho các tập hợp C = [1; 5], D = [-2; 3]. Hãy xác định tập hợp \(C \cap \;D\).
Lời giải chi tiết:
Ta có:

Giao của hai tập hợp C và D là \(C \cap \;D = \left[ {1;3} \right]\).
HĐ8
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên tham gia Chuyên đề 1 hoặc Chuyên đề 2.
Lời giải chi tiết:
Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.
Luyện tập 6
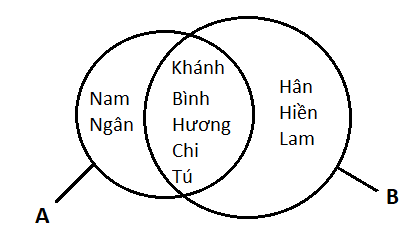
Hãy biểu diễn tập hợp \(A \cup \;\,B\) bằng biểu đồ Ven, với A, B được cho trong HĐ1
Lời giải chi tiết:
Ta có:
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Biểu đồ Ven
HĐ9
Trở lại tình huống mở đầu, hãy xác định tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2.
Lời giải chi tiết:
A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}
Luyện tập 7
Tìm phần bù của các tập hợp sau trong \(\mathbb{R}\):
a) \(\left( { - \infty ; - 2} \right)\)
b) \([ - 5; + \infty )\)
Phương pháp giải:
Biểu diễn các tập hợp trên trục số.
Lời giải chi tiết:
Ta có:

Suy ra phần bù của tập hợp \(\left( { - \infty ; - 2} \right)\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}\left( { - \infty ; - 2} \right) = [ - 2; + \infty )\)

Suy ra phần bù của tập hợp \([ - 5; + \infty )\) trong \(\mathbb{R}\) là: \(\mathbb{R}{\rm{\backslash }}[ - 5; + \infty ) = ( - \infty ; - 5)\)
Vận dụng
Lớp 10A có 24 bạn tham gia thi đấu bóng đá và cầu lông, trong đó có 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông. Giả sử các trận bóng đá và cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cầu lông?
Phương pháp giải:
Gọi x là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Sử dụng biểu đồ Ven để mô tả các tập hợp.
Lời giải chi tiết:
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
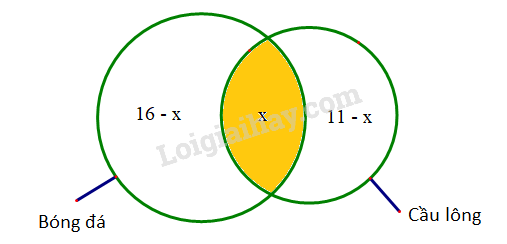
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.
