HĐ 4
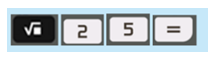
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút
Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút
Em hãy đọc kết quả x trên màn hình rồi tính x2.
Phương pháp giải:
Dùng máy tính cầm tay thao tác như đề bài.
Lời giải chi tiết:
a) Kết quả trên màn hình là: 5
Suy ra: \({x^2} = {5^2} = 25\)
b) Kết quả trên màn hình là: \(1,41421...\)
Suy ra: \({x^2} = 2\)
Thực hành 4
Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
\(\sqrt 3 ;\,\sqrt {15\,\,129} ;\,\sqrt {10\,\,000} ;\,\sqrt {10} \).
Phương pháp giải:
Dùng máy tính cầm tay để tính các căn bậc hai số học đã cho
Lời giải chi tiết:
\(\sqrt 3 \approx 1,732...;\,\sqrt {15\,\,129} \, = 123;\,\,\,\,\,\,\sqrt {10\,\,000} = 100;\,\,\,\sqrt {10} \approx 3,162...\)
Vận dụng 3
Dùng máy tính cầm để:
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2
b) Công thức tính diện tích S của hình tròn bán kính R là \(S = \pi {R^2}\). Tính bán kính của một hình tròn có diện tích là 100 cm2.
Phương pháp giải:
a) Độ dài cạnh bằng căn bậc hai số học của diện tích.
b) Áp dụng công thức: \(R = \sqrt {\frac{S}{\pi }} \)
Lời giải chi tiết:
a) Độ dài cạnh của một mảnh đất hình vuông là:
\(\sqrt {12\,\,996} = 114\)(m)
b) Bán kính của hình tròn là:
\(S = \pi {R^2} \Rightarrow R^2 = \frac{S}{\pi } \Rightarrow R = \sqrt {\frac{S}{\pi }} = \sqrt {\frac{{100}}{\pi }} \approx 5,64\)(cm)