Luyện tập
Cho hypebol (H) có một đỉnh là \({A_1}( - 4;0)\) và tiêu cự là 10. Viết phươn trình chính tắc và vẽ hypebol (H).
Lời giải chi tiết:
Hypebol (H) có một đỉnh là \({A_1}( - a;0) = ( - 4;0) \Rightarrow a = 4\)
Tiêu cự \(2c = 10 \Rightarrow c = 5 \Rightarrow b = \sqrt {{c^2} - {a^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{{4^2}}} - \frac{{{y^2}}}{{{3^2}}} = 1\)
* Vẽ hypebol
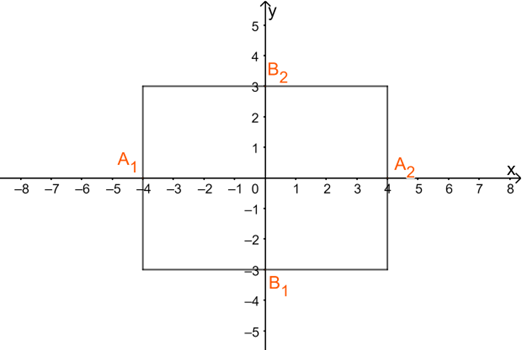
Bước 1: Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc 4 đường thẳng \(x = - 4,x = 4,y = 3,y = - 3\)
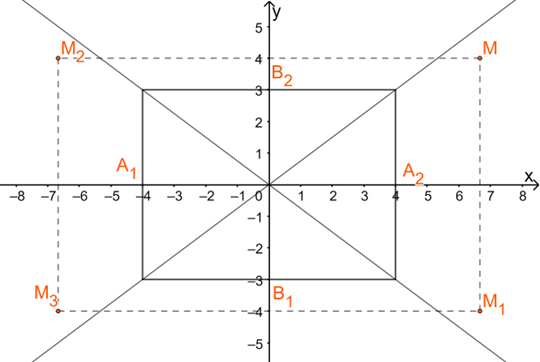
Bước 2: Vẽ hai đường chéo của hình chữ nhật sơ sở. Điểm \(M(\frac{{20}}{3};4)\) thuộc (H). Do đó các điểm \({M_1}(\frac{{20}}{3}; - 4),{M_2}( - \frac{{20}}{3};4),{M_3}( - \frac{{20}}{3}; - 4)\) thuộc (H).
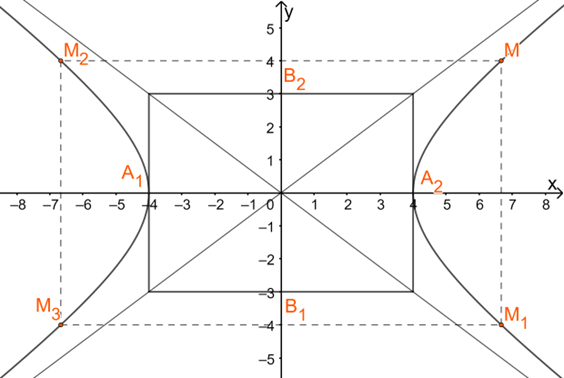
Bước 3: Vẽ hypebol