Hoạt động 1
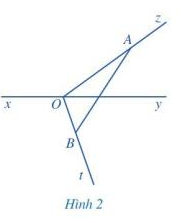
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy, ta vẽ hai tia Oz và Ot như Hình 2.
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Phương pháp giải:
Vẽ hình và nhận xét
Lời giải chi tiết:
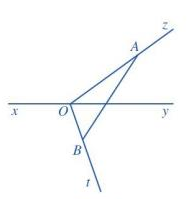
a)
b) Đoạn thẳng AB cắt đường thẳng xy
Hoạt động 2
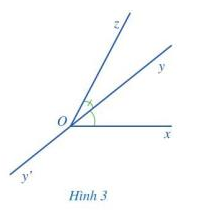
Quan sát hai góc xOy và zOy ở Hình 3.
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
Phương pháp giải:
Xác định đỉnh, cạnh của hai góc được đánh dấu rồi nhận xét.
+ Vẽ hình và nhận xét
Lời giải chi tiết:
a) Đỉnh của góc xOy và zOy cùng là đỉnh O; cạnh chung là cạnh Oy.
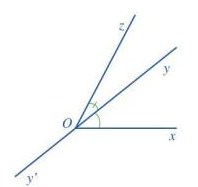
b)
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’
Luyện tập vận dụng 1
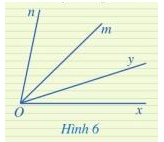
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
Phương pháp giải:
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Lời giải chi tiết:
Hai góc xOy và mOn không phải là hai góc kề nhau vì không có cạnh nào chung.
Luyện tập vận dụng 2
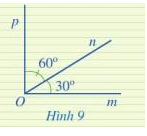
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
Phương pháp giải:
2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
Tính chất 2 góc kề nhau
Lời giải chi tiết:
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)