Hoạt động 3
Tìm tổng số đo của góc 110 \(^\circ \) và 70 \(^\circ \)
Phương pháp giải:
Tìm tổng số đo của góc
Lời giải chi tiết:
2 góc có tổng số đo là: 110 \(^\circ \)+70 \(^\circ \) = 180 \(^\circ \)
Hoạt động 4
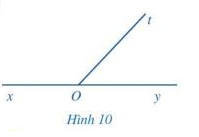
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
Phương pháp giải:
a) 2 góc có đỉnh chung, có một cạnh chung, hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó là hai góc kề nhau
b) Dựa vào tính chất 2 góc kề nhau, tính tổng số đo
Lời giải chi tiết:
a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\)
Mà \(\widehat {xOy} = 180^\circ \) ( góc bẹt)
\( \Rightarrow \widehat {xOt} + \widehat {yOt} = 180^\circ \)
Chú ý:
Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng
Luyện tập vận dụng 3
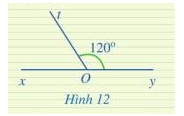
Tính góc xOt trong Hình 12
Phương pháp giải:
Sử dụng tính chất : Tổng số đo của 2 góc kề bù bằng 180 độ
Lời giải chi tiết:
Ta có: \(\widehat {xOt} + \widehat {tOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {xOt} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {xOt} = 180^\circ - 120^\circ = 60^\circ \end{array}\)