Đề bài
Bài 1: Tìm m để hệ phương trình sau có nghiệm duy nhất :
\(\left\{ \matrix{
3x{\rm{ }} - {\rm{ }}2y{\rm{ }} = {\rm{ }}6 \hfill \cr
mx{\rm{ }} + {\rm{ }}y{\rm{ }} = {\rm{ }}3 \hfill \cr} \right.\)
Bài 2: Cho hệ phương trình :
\(\left\{ \matrix{
3x + y = 5 \hfill \cr
5x - y = 11 \hfill \cr} \right.\)
a) Minh họa hình học tập nghiệm của mỗi phương trình trên cùng một hệ trục tọa độ.
b) Xác định nghiệm của hệ.
LG bài 1
Phương pháp giải:
Ta rút y từ hai phương trình và cho vế phải bằng nhau từ đó giải ra ta tìm được m
Lời giải chi tiết:
Bài 1: Viết lại hệ : \(\left\{ \matrix{ y = {3 \over 2}x - 3 \hfill \cr y = - mx + 3 \hfill \cr} \right.\)
Hệ có nghiệm duy nhất => Hai đường thẳng \(y = {3 \over 2}x - 3\) và \(y = - mx + 3\) cắt nhau
\( - m \ne {3 \over 2} \Leftrightarrow m \ne - {3 \over 2}.\)
LG bài 2
Lời giải chi tiết:
\( - m \ne {3 \over 2} \Leftrightarrow m \ne - {3 \over 2}.\)
Bài 2:
a) Vẽ đường thẳng (d1) : \(y = −3x + 5\)
Bảng giá trị :
|
x |
0 |
2 |
|
y |
5 |
−1 |
Đường thẳng (d1) qua hai điểm : \(A( 0; 5)\) và \(B( 2; −1).\)
Vẽ đường thẳng (d2) : \(y = 5x – 11.\)
Bảng giá trị :
|
x |
1 |
2 |
|
y |
−6 |
− 1 |
Đường thẳng ( d2) qua hai điểm : \(C(1; − 6)\) và \(B(2; − 1).\)
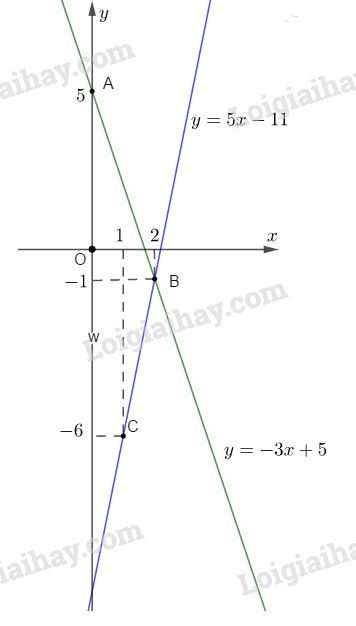
b) Phương trình hoành độ giao điểm của (d1) và (d2):
\( - 3x + 5 = 5x - 11 \Leftrightarrow 8x = 16 \)
\(\Leftrightarrow x = 2\)
Với \(x = 2 \Leftrightarrow y = − 1\).
Vậy nghiệm của hệ là \(( 2; − 1).\)
soanvan.me
