Đề bài
Câu 1 (2 điểm). Chọn khẳng định đúng
Cho hai đường tròn (O ; 3cm) và (O’ ; 5cm). Biết khoảng cách giữa hai tâm O và O’ bằng 4 cm. Khi đó, số điểm chung của hai đường tròn này là
(A) 0 (B) 1
(C) 2 (D) 3
Câu 2 (2 điểm). Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai ?
(A) AB là đường trung trực của OO’
(B) OO’ vuông góc với AB tại trung điểm của đoạn thẳng AB
(C) AB là tia phân giác của góc OAO’
(D) \(\widehat {AOO'} = \widehat {BOO'}\)
Câu 3 (6 điểm). Cho đường tròn (O ; 4cm) và đường thẳng d, độ dài đường vuông góc OH từ O đến d bằng 8cm.
a) Hãy xác định vị trí tương đối giữa đường tròn (O) và đường thẳng d
b) Gọi A là một điểm bất kì thuộc d. Kẻ các tiếp tuyến AB và AC của (O); B và C là các tiếp điểm. Đoạn thẳng BC cắt OA và OH lần lượt tại I và K. Chứng minh các tam giác OIK và OHA đồng dạng.
c) Tính tích OI.OA.
Lời giải chi tiết
Câu 1:
Phương pháp giải:
Tìm \(OO'\) và tổng hoặc hiệu của hai bán kính rồi so sánh theo bảng sau:
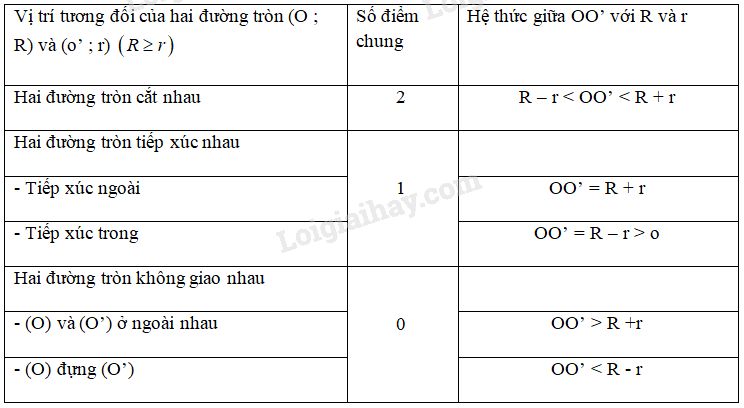
Lời giải :
Ta có : \(OO' = 4cm\)
\(R + r = 5 + 3 = 8cm\)
\(R - r = 5 - 3 = 2cm\)
Vì \(R - r < OO' < R + r\) nên hai đường tròn cắt nhau.
Khi đó số điểm chung của hai đường tròn này là \(2.\)
Chọn C.
Câu 2:
Phương pháp giải :
Vận dụng kiến thức : Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây cung chung.
Lời giải :
Trong các nhận xét đã cho, nhận xét \(AB\) là tia phân giác của \(OAO'\) là sai.
Chọn C.
Câu 3:
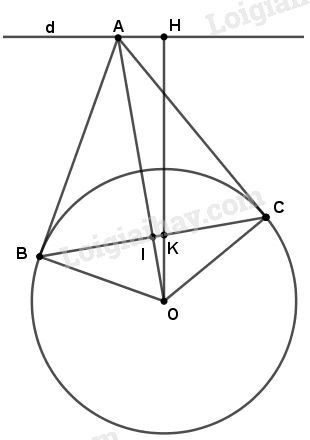
Phương pháp giải :
a) Vận dụng kiến thức : Cho đường thẳng a và đường tròn (O ; R). Gọi d là khoảng cách từ O đến a. Ta có:
- a cắt (O) \( \Leftrightarrow d < R\)
- a tiếp xúc với (O) \( \Leftrightarrow d = R\)
- a không giao với (O) \( \Leftrightarrow d > R\)
b) Chứng minh các tam giác là tam giác vuông có chung góc nhọn.
c) Sử dụng hệ thức lượng trong tam giác vuông.
Lời giải :
a) Đường tròn tâm \(O\) có bán kính bằng \(4cm.\)
Đường thẳng \(d\) cách \(O\) một khoảng bằng \(8cm.\)
Vì \(8 > 4\) nên \(d\) không giao nhau với \(\left( O \right).\)
b) Tam giác \(AHO\) có \(OH \bot AH\) (cách vẽ)
Tam giác \(IKO\) có \(OI \bot IK\) (tính chất hai tiếp tuyến cắt nhau)
Xét tam giác \(AHO\) và tam giác \(IKO\) có :
\(\widehat {AOH}\) là góc chung
\(\widehat {AHO} = \widehat {IOK} = {90^o}\) (chứng minh trên)
Vậy \(\Delta AHO \backsim \Delta IKO\left( {g . g} \right)\)
c) Vì \(AB,AC\) là hai tiếp tuyến của đường tròn \((O)\) nên \(AB=AC\) (tính chất hai tiếp tuyến cắt nhau)
Lại có \(OB=OC=4cm\) nên \(OA\) là đường trung trực của \(BC\) hay \(OA \bot BC\) tại \(I\)
Xét tam giác \(OCA\) vuông tại \(C\) có \(OI\) là đường cao ứng với cạnh \(OA\), theo hệ thức lượng trong tam giác vuông ta có: \(OC^2=OI.OA\) hay \(OI.OA=16\)
soanvan.me
