Đề bài
Bài 1. Cho tam giác ABC cân tại A có \(AB = AC = 1\;cm\) và góc \(A = 2α (0 < α < 45^o)\), các đường cao AD và BE.
a. Chứng minh rằng : ∆ADC và ∆BEC đồng dạng
b. Chứng minh : \(\sin A = 2\sinα.\cosα\)
Bài 2. Cho ∆ABC vuông tại A và \(AC = 21cm\), \(\cos \widehat C = {3 \over 5}\)
a. Tính \(\tan B, \cot B\).
b. Đường phân giác của góc A cắt cạnh BC tại D. Tính \(DB, DC\)
LG bài 1
Phương pháp giải:
Sử dụng tam giác đồng dạng và quan hệ giữa cạnh và góc trong tam giác vuông.
Trong một tam giác vuông, mỗi cạnh góc vuông bằng: Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Lời giải chi tiết:
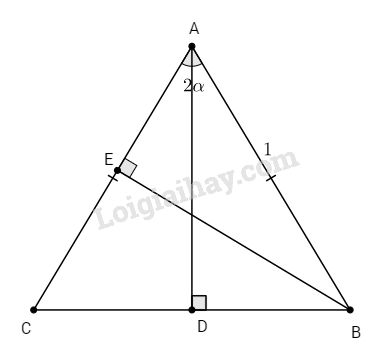
a. Xét tam giác ADC và tam giác BEC có góc C chung và \(\widehat D = \widehat E = {90^0}\) nên ∆ADC đồng dạng ∆BEC (g.g)
b. ∆ABC cân tại A nên đường cao AD đồng thời là đường phân giác \(\widehat {BAD} = \widehat {CAD} = {{\widehat A} \over 2} = \alpha \)
Xét tam giác vuông ADB có:
\(BD = AB.\sin \widehat {BAD} = 1.\sin \alpha = \sin \alpha \)
Mặt khác ∆ABC cân nên đường cao AD cũng đồng thời là đường trung tuyến hay BC = 2BD = 2sinα
Xét tam giác vuông CEB có \(\widehat {CBE} = \widehat {CAD} = \alpha \) (cùng phụ với góc C)
Ta có: \(BE = BC.\cos \widehat {CBE} = BC.\cos \alpha \)\(\;= 2\sin \alpha .\cos \alpha \) (1)
Xét tam giác vuông AEB, ta có: \(\sin A = {{BE} \over {AB}} = {{BE} \over 1} = BE\) (2)
Từ (1) và (2) ⇒ sinA = 2sinα.cosα
LG bài 2
Phương pháp giải:
Sử dụng:
+) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\)
+) Định lý Pytago và tính chất đường phân giác của tam giác.
Lời giải chi tiết:
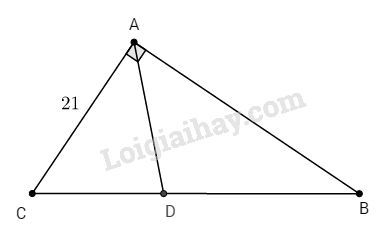
a. Ta có:
\(\eqalign{ & {\sin ^2}C + {\cos ^2}C = 1 \cr & \Rightarrow \sin C = \sqrt {1 - {{\cos }^2}C} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sqrt {1 - {{\left( {{3 \over 5}} \right)}^2}} = {4 \over 5} \cr} \)
Do đó:
\(\eqalign{ & \cos B = {4 \over 5} \cr & \cos C = {3 \over 5} \cr} \)
\( \Rightarrow \sin B = {3 \over 5}\) (vì góc B và góc C là hai góc phụ nhau)
Vậy \(\tan B = {{\sin B} \over {\cos B}} = {3 \over 5}:{4 \over 5} = {3 \over 4} \)\(\Rightarrow \cot B = {4 \over 3}\)
Cách khác tính tanB (gần gũi hơn) :
\(\eqalign{ & \cos C = {{AC} \over {BC}}\,hay\,{3 \over 5} = {{21} \over {BC}}\cr& \Rightarrow BC = {{21.5} \over 3} = 35 \cr & \Rightarrow AB = \sqrt {B{C^2} - A{C^2}} \cr&\;\;\;\;\;\;\;\;\;\;\;= \sqrt {{{35}^2} - {{21}^2}} = 28 \cr} \)
Do đó: \(\tan B = {{AC} \over {AB}} = {{21} \over {28}} = {3 \over 4}\)
b. Ta có: ∆ABC vuông tại A:
\( AB = AC.\tan C = AC.cotB \)\(\;= 21.{4 \over 3} = 28\,\left( {cm} \right) \)
và \(\,BC = {{AC} \over {\cos C}} = {{21} \over {{3 \over 5}}} = 35\,\left( {cm} \right) \)
AD là phân giác của ∆ABC ta có:
\({{DB} \over {DC}} = {{AB} \over {AC}} = {{28} \over {21}} = {4 \over 3} \)
\(\Rightarrow {{DB} \over 4} = {{DC} \over 3} = {{DB + DC} \over {4 + 3}} \)\(\;= {{BC} \over 7} = {{35} \over 7} = 5\)
Vậy \(DB = 5.4 = 20 (cm)\); \(DC = 5.3 = 15 (cm)\).
soanvan.me
