LG bài 3
Bài 1. Không dùng bảng số và máy tính , hãy tính:
\(A = 3\tan 67^\circ + 5{\cos ^2}16^\circ - 3\cot 23^\circ \)\(\;+ 5{\cos ^2}74^\circ - {{\cot 37^\circ } \over {\tan 53^\circ }}\)
Bài 2. Cho tam giác ABC vuông tại C có \({\mathop{\rm sinA}\nolimits} = {3 \over 5}\). Không tính số đo góc A. Hãy tính cosA, tanA, cotA.
Bài 3. Cho tam giác ABC. Chứng minh rằng \({S_{ABC}} = {1 \over 2}AB.AC.\sin A\)
Bài 4. Cho tam giác ABC vuông tại A có \(AB = 9cm, \;BC = 15cm\), đường cao AH.
a. Tính AH và CH.
b. Qua B vẽ đường thẳng vuông góc với BC cắt đường thẳng AC tại D. Tia phân giác của góc C cắt AB tại N và BD tại M. Chứng minh \(CN.CD = CM.CB\)
c. Chứng minh \({{NA} \over {MD}} = {{CA} \over {CD}}\)
(Tính độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ nhất, nếu có).
LG bài 1
Phương pháp giải:
Sử dụng:
+) Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
+) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Lời giải chi tiết:
Ta có:
\(\eqalign{ A &= 3\tan 67^\circ + 5{\cos ^2}16^\circ - 3\cot 23^\circ + 5{\cos ^2}74^\circ - {{\cot 37^\circ } \over {\tan 53^\circ }} \cr & = 3\tan 67^\circ - 3\cot 23^\circ + 5{\cos ^2}16^\circ + 5{\cos ^2}74^\circ - {{\cot 37^\circ } \over {\tan 53^\circ }} \cr & = 3\tan 67^\circ - 3\tan 67^\circ + 5{\cos ^2}16^\circ + 5{\sin ^2}16 - {{\tan 53^\circ } \over {\tan 53^\circ }} \cr & = 0 + 5\left( {{{\cos }^2}16^\circ + {{\sin }^2}16^\circ } \right) - 1 = 5 - 1 = 4 \cr} \)
LG bài 2
Phương pháp giải:
Sử dụng:
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat C =\alpha\). Ta có:
\(\sin \alpha = \dfrac{{cạnh\,đối}}{{cạnh\,huyền}} = \dfrac{{AB}}{{BC}};\)\(\cos \alpha = \dfrac{{cạnh\,kề}}{{cạnh\,huyền}} = \dfrac{{AC}}{{BC}}\)
\(\tan \alpha = \dfrac{{cạnh\, đối}}{{cạnh\,kề}} = \dfrac{{AB}}{{AC}};\)\(\cot \alpha = \dfrac{{cạnh\,kề}}{{cạnh\,đối}} = \dfrac{{AC}}{{AB}}\)
\(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
Lời giải chi tiết:
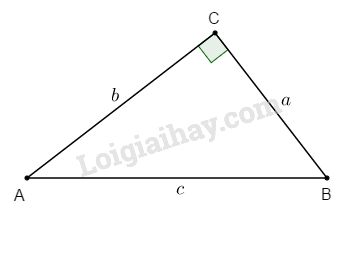
\(\sin A = {3 \over 5}\) hay \({a \over c} = {3 \over 5} \Rightarrow a = {{3c} \over 5} \Rightarrow {a^2} = {{9{c^2}} \over {25}}\)
Theo định lí Pi-ta-go, ta có:
\(\eqalign{ & {b^2} = {c^2} - {a^2} = {c^2} - {{9{c^2}} \over {25}} = {{16{c^2}} \over {25}} \cr & \Rightarrow b = {4 \over 5}c \Rightarrow {b \over c} = {4 \over 5} \cr} \)
Vậy \(\cos A = {4 \over 5},\,tanA = {3 \over 4},\,\cot A = {4 \over 3}\)
Cách khác : Ta có: \({\sin ^2}A + {\cos ^2}A = 1 \)\(\,\Rightarrow {\cos ^2}A = 1 - {\sin ^2}A\)
\(\eqalign{ & \Rightarrow \cos A = \sqrt {1 - {{\sin }^2}A} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {1 - {{\left( {{3 \over 5}} \right)}^2}} = \sqrt {{{16} \over {25}}} = {4 \over 5} \cr & \tan A = {{\sin A} \over {\cos A}} = {3 \over 5}:{4 \over 5} = {3 \over 4}\cr&\cot A= \dfrac{1}{{\tan A}} = {4 \over 3} \cr} \)
LG bài 3
Phương pháp giải:
Trong một tam giác vuông, mỗi cạnh góc vuông bằng: Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Diện tích tam giác bằng nửa tích chiều cao và cạnh đáy tương ứng
Lời giải chi tiết:
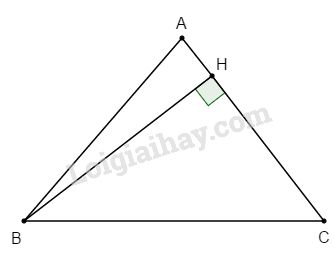
Kẻ đường cao BH của tam giác ABC
Xét tam giác vuông AHB ta có: \(BH = AB.\sin A\)
\( \Rightarrow {S_{ABC}} = {1 \over 2}AC.BH\)\(\; = {1 \over 2}AB.AC.\sin A\)
LG bài 4
Phương pháp giải:
Sử dụng:
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Khi đó ta có các hệ thức sau:
+) \(A{B^2} = BH.BC\) và \(A{C^2} = CH.BC\
+) \(H{A^2} = HB.HC\)
+) \(AB.AC = BC.AH\)
+) \(B{C^2} = A{B^2} + A{C^2}\) (Định lí Pitago).
Lời giải chi tiết:
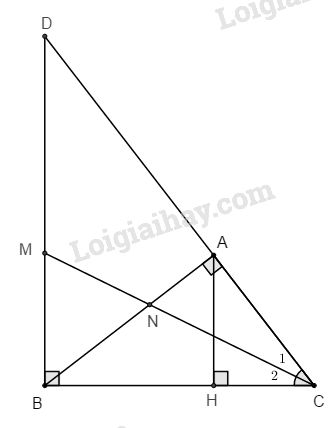
a. Theo định lí Pi-ta-go, ta có:
\(A{C^2} = B{C^2} - A{B^2} = {15^2} - {9^2} = 144\)
\(\Rightarrow AC = 12\,\left( {cm} \right)\)
Tam giác ABC vuông tại A có đường cao AH, ta có:
\(AH.BC = AB.AC\) (hệ thức lượng)
\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{9.12} \over {15}} = 7,2\,\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông, ta có:
\(A{C^2} = BC.CH \)
\(\Rightarrow CH = {{A{C^2}} \over {BC}} = {{{{12}^2}} \over {15}} = 9,6\,\left( {cm} \right)\)
b. Ta có: \({\widehat C_1} = {\widehat C_2}\) (giả thiết)
⇒ ∆CAN đồng dạng ∆CBM (g.g)
\( \Rightarrow {{CN} \over {CM}} = {{CA} \over {CB}}\) (1)
Dẽ thấy ∆CAB đồng dạng ∆CBD (g.g)
\( \Rightarrow {{CA} \over {CB}} = {{CB} \over {CD}}\) (2)
Từ (1) và (2) \( \Rightarrow {{CN} \over {CM}} = {{CB} \over {CD}} \Rightarrow CN.CD = CM.CB\)
c. ∆CAN đồng dạng ∆CBM (chứng minh trên), ta có: \({{NA} \over {CA}} = {{MB} \over {CM}}\) (3)
Tia CM là phân giác của ∆CBD \( \Rightarrow {{MB} \over {MD}} = {{CB} \over {CD}} \Rightarrow {{MB} \over {CB}} = {{MD} \over {CD}}\) (4)
Từ (3) và (4) \( \Rightarrow {{NA} \over {CA}} = {{MD} \over {CD}} \Rightarrow {{NA} \over {MD}} = {{CA} \over {CD}}\)
soanvan.me
