- A
Cân bằng bền
- B
Cân bằng không bền
- C
Cân bằng phiếm định
- D
Không dạng cân bằng nào cả
Đáp án: A
Phương pháp giải:
Vận dụng lí thuyết về các dạng cân bằng
Lời giải chi tiết:
Lật đật được chế tạo ở trạng thái cân bằng bền: Toàn bộ thân hình con lật đật đều rất nhẹ chỉ có phần đáy của nó có một vật tương đối nặng - một miếng chì hoặc miếng thép. Vì thế, trọng tâm của nó rất thấp. Mặt khác diện tích đáy của con lật đật vừa to lại vừa tròn nhẵn dễ dao động. Độ nghiêng của con lật đật càng lớn, khoảng cách mà điểm tựa cách xa trọng tâm càng lớn, thế năng dao động do trọng lượng sinh ra sẽ theo đó mà tăng lên khiến xu thế khôi phục lại vị trí cũ của nó cũng càng rõ rệt.
Câu hỏi 2 :
Một viên đá đang nằm yên trên mặt đất, lực hấp dẫn do Trái Đất tác dụng vào hòn đá có giá trị:
- A
lớn hơn trọng lượng của hòn đá.
- B
nhỏ hơn trọng lượng của hòn đá.
- C
bằng trọng lượng của hòn đá
- D
bằng 0.
Đáp án: C
Lời giải chi tiết:
Ta có, viên đá nằm yên trên mặt đất => \(h{\rm{ }} = {\rm{ }}0\)
+ Trọng lượng của viên đá: \(P = G\frac{{mM}}{{{R^2}}}\)
+ Lực hấp dẫn do Trái Đất tác dụng vào viên đá: \({F_{h{\rm{d}}}} = G\frac{{mM}}{{{R^2}}}\)
=> Lực hấp dẫn do Trái Đất tác dụng vào hòn đá bằng với trọng lượng của hoàn đá
Câu hỏi 3 :
Chọn phát biểu đúng. Trong các chuyển động tròn đều
- A
chuyển động nào có chu kì quay nhỏ hơn, thì tốc độ góc lớn hơn.
- B
chuyển động nào có chu kì quay lớn hơn, thì có tốc độ góc lớn hơn
- C
chuyển động nào có tần số lớn hơn, thì có tốc độ góc nhỏ hơn.
- D
có cùng chu kì, thì chuyển động nào có bán kính nhỏ hơn thì có tốc độ góc lớn hơn.
Đáp án: A
Phương pháp giải:
+ Vận dụng biểu thức tính tốc độ góc: \(\omega = \frac{{2\pi }}{T}\)
+ Vận dụng biểu thức tính tần số: \(f = \frac{1}{T}\)
+ Vận dụng biểu thức tính vận tốc dài: \(v = \omega r\)
Lời giải chi tiết:
Ta có: Tốc độ góc: \(\omega = \dfrac{{2\pi }}{T} = 2\pi f\)
Tốc độ góc tỉ lệ thuận với tần số và tỉ lệ nghịch với chu kì
=> Chuyển động nào có chu kì nhỏ hay tần số lớn thì tốc độ góc lớn và ngược lại, chuyển động nào có chu kì lớn hay tần số nhỏ thì tốc độ góc nhỏ.
Câu hỏi 4 :
Chuyển động thẳng biến đổi đều là chuyển động
- A
Có quỹ đạo là đường thẳng, có véctơ gia tốc và vận tốc không thay đổi trong suốt quá trình chuyển động.
- B
Có quỹ đạo là đường thẳng, véctơ gia tốc bằng không
- C
Có quỹ đạo là đường thẳng, véctơ gia tốc không thay đổi trong suốt quá trình chuyển động.
- D
Có quỹ đạo là đường thẳng, véctơ vận tốc không thay đổi trong suốt quá trình chuyển động.
Đáp án: C
Lời giải chi tiết:
Chuyển động thẳng biến đổi là chuyển động thẳng trong đó gia tốc tức thời không đổi
- Ta để ý rằng khái niệm vectơ vận tốc không đổi nghĩa là trong suốt quá trình chuyển động cả độ lớn và phương chiều của vận tốc là không thay đổi điều này không phù hợp với chuyển động thẳng biến đổi đều có độ lớn vận tốc là một hàm bậc nhất của thời gian
Câu hỏi 5 :
Sự xuất hiện của lực nào sau đây không phải là lực đàn hồi
- A
Lực xuất hiện khi dương cánh cung
- B
Lò xo giảm xóc ở xe máy
- C
Đệm mút của giường nằm
- D
Lực hút của nam châm dính trên bảng từ
Đáp án: D
Phương pháp giải:
Vận dụng định nghĩa về lực đàn hồi: Lực đàn hồi là lực sinh ra khi vật đàn hồi bị biến dạng. Lực đàn hồi có xu hướng chống lại nguyên nhân sinh ra nó.
Lời giải chi tiết:
Ta có: Lực đàn hồi là lực sinh ra khi vật đàn hồi bị biến dạng. Lực đàn hồi có xu hướng chống lại nguyên nhân sinh ra nó. Vì vậy trong các lực trên sự xuất hiện của lực hút của nam châm dính trên bảng từ không phải là lực đàn hồi.
Câu hỏi 6 :
Mômen lực được xác định bằng công thức:
- A
\(F = ma\)
- B
\(M = \dfrac{F}{d}\)
- C
\(P = mg\)
- D
\(M = F{\rm{d}}\)
Đáp án: D
Lời giải chi tiết:
Xét một lực \(\overrightarrow F \) nằm trong mặt phẳng vuông góc với trục quay Oz. Momen của lực \(\overrightarrow F \) đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực quanh trục ấy và được đo bằng tích độ lớn của lực với cánh tay đòn.
\(M = F{\rm{d}}\)
Câu hỏi 7 :
Câu nào sau đây nói về sự rơi là đúng?
- A
Khi không có sức cản, vật nặng rơi nhanh hơn vật nhẹ.
- B
Ở cùng một nơi, mọi vật rơi tự do có cùng gia tốc.
- C
Khi rơi tự do, vật nào ở độ cao hơn sẽ rơi với gia tốc lớn hơn.
- D
Vận tốc của vật chạm đất, không phụ thuộc vào độ cao của vật khi rơi.
Đáp án: B
Lời giải chi tiết:
A – sai vì: Khi không có sức cản, các vật nặng nhẹ đều rơi như nhau
B – đúng
C – sai vì: Các vật rơi tự do với gia tốc như nhau
D – sai vì: Vận tốc của vật chạm đất phụ thuộc vào độ cao của vật khi rơi
Câu hỏi 8 :
Biểu thức nào sau đây là đúng về định luật III – Niuton?
- A
\(\overrightarrow {{F_{AB}}} = \overrightarrow {{F_{BA}}} \)
- B
\(\overrightarrow {{F_{AB}}} + \overrightarrow {{F_{BA}}} = \overrightarrow 0 \)
- C
$\dfrac{{\overrightarrow {{F_{AB}}} }}{{\overrightarrow {{F_{BA}}} }} = \overrightarrow 0 $
- D
$\overrightarrow {{F_{AB}}} .\overrightarrow {{F_{BA}}} = \overrightarrow 0 $
Đáp án: B
Phương pháp giải:
Sử dụng lý thuyết về định luật III – Niuton: Khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng trở lại vật A một lực. Hai lực này là hai lực trực đối:
Lời giải chi tiết:
Định luật III - Niutơn: Khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng trở lại vật A một lực. Hai lực này là hai lực trực đối: ${\vec F_{AB}} = - {\vec F_{BA}}$
Nên ta có:\(\overrightarrow {{F_{AB}}} + \overrightarrow {{F_{BA}}} = 0\)
Câu hỏi 9 :
Một máy bay đang bay thẳng đều ở độ cao h với tốc độ \({v_0}\) thì thả rơi một vật. Khi vật chạm đất, vật cách chỗ thả vật một đoạn bao nhiêu? Bỏ qua sức cản của không khí)
- A
\(s = {v_0}\sqrt {\dfrac{{2h}}{g}} \)
- B
\(s = 2{v_0}\sqrt {gh} \)
- C
\(s = {v_0}\dfrac{{2h}}{g}\)
- D
\(s = \dfrac{{2gh}}{{{v_0}}}\)
Đáp án: A
Phương pháp giải:
Sử dụng các công thức của chuyển động ném ngang: Tầm xa: \(L = v\sqrt {\dfrac{{2h}}{g}} \)
Lời giải chi tiết:
Tầm xa: \(L = v_0\sqrt {\dfrac{{2h}}{g}} \)
Vậy khi vật chạm đất, vật cách chỗ thả vật một đoạn \(L = v_0\sqrt {\dfrac{{2h}}{g}} \)
Câu hỏi 10 :
Câu nào dưới đây nói về chuyển động thẳng biến đổi đều là không đúng?
- A
Vận tốc tức thời của chuyển động thẳng biến đổi đều có độ lớn tăng hoặc giảm dần đều theo thời gian.
- B
Gia tốc của vật chuyển động thẳng biến đổi đều có độ lớn không đổi.
- C
Gia tốc của vật chuyển động thẳng biến đổi đều luôn cùng phương, chiều với vận tốc.
- D
Quãng đường đi được của vật chuyển động thẳng biến đổi đều luôn được tính theo công thức \(s = {v_{tb}}.t\), với \({v_{tb}}\) là vận tốc trung bình của vật.
Đáp án: C
Lời giải chi tiết:
A, B, D – đúng
C – sai vì: khi vật chuyển động chậm dần đều gia tốc và vận tốc ngược chiều với nhau.
Câu hỏi 11 :
Điều nào sau đây là đúng khi nói về lực tác dụng lên vật chuyển động tròn đều?
- A
Vật chỉ chịu tác dụng của một lực duy nhất
- B
Hợp lực của tất cả các lực tác dụng lên vật đóng vai trò là lực hướng tâm
- C
Ngoài các lực cơ học, vật còn chịu thêm tác dụng của lực hướng tâm
- D
Hợp lực của tất cả các lực tác dụng lên vật nằm theo phương tiếp tuyến với quỹ đạo.
Đáp án: B
Lời giải chi tiết:
Ta có: Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm gọi là lực hướng tâm.
=> Các phương án:
A - sai vì vật có thể chịu tác dụng của nhiều lực
B - đúng
C - sai vì lực hướng tâm không phải là lực mới
D - sai vì hợp lực của tất cả các lực tác dụng lên vật hướng vào tâm
Câu hỏi 12 :
Vận tốc của chất điểm trong chuyển động thẳng đều
- A
Không thay đổi cả về dấu và độ lớn
- B
Phụ thuộc bậc nhất vào thời gian
- C
Có độ lớn thay đổi và có dấu không đổi
- D
Có độ lớn không đổi và có dấu thay đổi
Đáp án: A
Lời giải chi tiết:
Vận tốc của chất điểm trong chuyển động thẳng đều không thay đổi cả về dấu và độ lớn
Câu hỏi 13 :
Lực ma sát nghỉ xuất hiện khi:
- A
có ngoại lực tác dụng lên vật. Ngoại lực này có xu hướng làm cho vật chuyển động và đủ để thắng lực ma sát.
- B
có nội lực tác dụng lên vật. Nội lực này có xu hướng làm cho vật chuyển động nhưng chưa đủ để thắng lực ma sát.
- C
có ngoại lực tác dụng lên vật. Ngoại lực này có xu hướng làm cho vật chuyển động nhưng chưa đủ để thắng lực ma sát.
- D
có nội lực tác dụng lên vật. Nội lực này có xu hướng làm cho vật chuyển động và đủ để thắng lực ma sát.
Đáp án: C
Lời giải chi tiết:
Lực ma sát nghỉ \(({\overrightarrow F _{m{\rm{s}}n}})\) chỉ xuất hiện khi có ngoại lực tác dụng lên vật. Ngoại lực này có xu hướng làm cho vật chuyển động nhưng chưa đủ để thắng lực ma sát.
Câu hỏi 14 :
Chuyển động thẳng đều là:
- A
Chuyển động thẳng, trong đó chất điểm có gia tốc không đổi.
- B
Chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
- C
Chuyển động có quỹ đạo là đường thẳng và gia tốc như nhau trên mọi quãng đường.
- D
Chuyển động thẳng, trong đó chất điểm có vận tốc tức thời thay đổi
Đáp án: B
Lời giải chi tiết:
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
Câu hỏi 15 :
Đâu là biểu thức đúng của lực quán tính:
- A
\(\overrightarrow {{F_{qt}}} = m\overrightarrow a \)
- B
\(\overrightarrow {{F_{qt}}} = - m\overrightarrow a \)
- C
\({\overrightarrow F _{qt}} = ma\)
- D
\({\overrightarrow F _{qt}} = - ma\)
Đáp án: B
Lời giải chi tiết:
\(\overrightarrow {{F_{qt}}} = - m\overrightarrow a \)
Trong đó:
+ \(m\): khối lượng của vật \(\left( {kg} \right)\)
+ \(a\): gia tốc của hệ quy chiếu chuyến động \(\left( {m/{s^2}} \right)\)
Câu hỏi 16 :
Một vật chuyển động dọc theo chiều (+) trục Ox với vận tốc không đổi, thì:
- A
tọa độ của vật luôn có giá trị (+)
- B
vận tốc của vật luôn có giá trị (+)
- C
tọa độ và vận tốc của vật luôn có giá trị (+)
- D
tọa độ luôn trùng với quãng đường
Đáp án: C
Lời giải chi tiết:
Một vật chuyển động dọc theo chiều (+) trục Ox với vận tốc không đổi, thì tọa độ và vận tốc của vật luôn có giá tri (+)
Còn quãng đường còn phụ thuộc xem vật xuất phát từ đâu
Câu hỏi 17 :
Một thang máy mang một người từ tầng trệt đi xuống tầng hầm sâu $5m$, rồi lên đến tầng $3$ . Biết rằng mỗi tầng cách nhau $4m$. Trục toạ độ có gốc và chiều dương như hình vẽ. Quãng đường chuyển động khi người này lên đến tầng $3$?
- A
$22 m$
- B
$17 m$
- C
$29 m$
- D
$34 m$
Đáp án: A
Phương pháp giải:
Xác định quãng đường thang máy chuyển động
Lời giải chi tiết:
Ta có: Thang máy di chuyển từ tầng trệt - tầng hầm - tầng trệt - tầng $1$ - tầng $2$ - tầng $3$:
Câu hỏi 18 :
Vật chuyển động thẳng có phương trình \(x = 2{t^2} - 4t + 10(m;s)\) . Vật sẽ dừng lại tại vị trí :
- A
x = 10m
- B
x = 4m
- C
x = 6m
- D
x = 8m
Đáp án: D
Phương pháp giải:
+ Vật dừng lại khi có vận tốc bằng 0 - Giải phương trình v = 0 để tìm thời gian t
+ Thay t vào phương trình chuyển động => vị trí dừng lại
Lời giải chi tiết:
Phương trình vận tốc của vật:
\(\begin{array}{l}v = - 4 + 4t\\v = 0 \leftrightarrow - 4 + 4t = 0 \to t = 1{\rm{s}}\end{array}\)
Vật sẽ dừng lại tại vị trí \(x = {2.1^2} - 4.1 + 10 = 8m\)
Câu hỏi 19 :
Cùng một lúc tại hai điểm A, B cách nhau \(125{\rm{ }}m\) có hai vật chuyển động ngược chiều nhau. Vật đi từ A có vận tốc đầu \(4{\rm{ }}m/s\) và gia tốc là \(2{\rm{ }}m/{s^2}\), vật đi từ B có vận tốc đầu \(6{\rm{ }}m/s\) và gia tốc \(4{\rm{ }}m/{s^2}\) . Biết các vật chuyển động nhanh dần đều. Chọn A làm gốc tọa độ, chiều dương hướng từ A đến B, gốc thời gian lúc hai vật cùng xuất phát. Hai vật gặp nhau tại vị trí cách A bao nhiêu?
- A
\(45m\)
- B
\(80m\)
- C
\(25m\)
- D
\(95m\)
Đáp án: A
Phương pháp giải:
+ Viết phương trình chuyển động của 2 xe
+ Giải phương trình \({x_1} = {\rm{ }}{x_2}\)
+ Thay t vào phương trình của 1 xe
Lời giải chi tiết:
Ta có:
Câu hỏi 20 :
Từ độ cao 20m, phải ném một vật thẳng đứng với vận tốc v0 bằng bao nhiêu để vật này tới mặt đất sớm hơn 1s so với vật rơi tự do
- A
\(15m/s\)
- B
\(24m/s\)
- C
\(12,5m/s\)
- D
\(22,4m/s\)
Đáp án: A
Phương pháp giải:
+ Viết phương trình chuyển động của mỗi vật
- Khi bị ném
- Khi rơi tự do
+ Vận dụng biểu thức: \({\rm{s}} = {v_0}t + \frac{1}{2}g{t^2}\)
Lời giải chi tiết:
Các phương trình chuyển động:
+ PT chuyển động rơi tự do: \({s_1} = \frac{1}{2}g{t^2} = 5{t^2}\) (1)
+ PT chuyển động khi vật bị ném: \({s_2} = {v_0}t' + \frac{1}{2}gt{'^2} = {v_0}t + 5t{'^2}\) (2)
Ta có, thời gian vật rơi tự do chạm đất:\({s_1} = 5{t^2} = 20 \to t = 2{\rm{s}}\)
Theo đề : \(t - t' = 1 \to t' = 1{\rm{s}}\)
Thay vào (2) ta được : \(20 = 5 + {v_0} \to {v_0} = 15m/s\)
Câu hỏi 21 :
Hai ô-tô cùng xuất phát từ hai bến xe A và B cách nhau 20km trên một đoạn đường thẳng. Nếu hai ô-tô chạy ngược chiều thì chúng sẽ gặp nhau sau \(15\) phút. Nếu hai ô-tô chạy cùng chiều thì chúng sẽ đuổi kịp nhau sau \(1\) giờ. Tính vận tốc của mỗi ô-tô.
- A
\(\left\{ \begin{array}{l}{v_{13}} = 30km/h\\{v_{23}} = 50km/h\end{array} \right.\)
- B
\(\left\{ \begin{array}{l}{v_{13}} = 20km/h\\{v_{23}} = 20km/h\end{array} \right.\)
- C
\(\left\{ \begin{array}{l}{v_{13}} = 25km/h\\{v_{23}} = 36km/h\end{array} \right.\)
- D
\(\left\{ \begin{array}{l}{v_{13}} = 50km/h\\{v_{23}} = 30km/h\end{array} \right.\)
Đáp án: D
Phương pháp giải:
Xác định các thông số:
+ Số 1: gắn với vật cần tính vận tốc
+ Số 2: gắn với hệ quy chiếu là các vật chuyển động
+ Số 3: gắn với hệ quy chiếu là các vật đứng yên
+ \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động
+ \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên
- Vận dụng công thức cộng vận tốc: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
- Vận dụng biểu thức: \(S = vt\)
Lời giải chi tiết:
(1) xe tại bến A
(2) xe tại bến B
(3) mặt đường
Ta có:
+ Thời gian gặp nhau khi 2 xe chạy ngược chiều: \({t_1} = 15p = 0,25h\)
+ Thời gian gặp nhau khi 2 xe chạy cùng chiều: \({t_2} = 1h\)
- Khi hai xe chuyển động ngược chiều, ta có: \({v_{12}} = {v_{13}} + {v_{23}} = \dfrac{{AB}}{{{t_1}}}\)
\( \Rightarrow {v_{13}} + {v_{23}} = \dfrac{{20}}{{0,25}} = 80\) (1)
- Khi hai xe chuyển động cùng chiều, ta có: \({v_{12}}' = {v_{13}} - {v_{23}} = \dfrac{{AB}}{{{t_2}}}\)
\( \Rightarrow {v_{13}} - {v_{23}} = \dfrac{{20}}{1} = 20\) (2)
Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}{v_{13}} = 50km/h\\{v_{23}} = 30km/h\end{array} \right.\)
Câu hỏi 22 :
Lực có môđun 30N là hợp lực của hai lực nào ?
- A
12N, 12N
- B
16N, 10N
- C
16N, 46N
- D
16N, 50N
Đáp án: C
Phương pháp giải:
Vận dụng điều kiện của hợp lực: \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)
Lời giải chi tiết:
Ta có, điều kiện của hợp lực: \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)
Phương án A : \(0 \le F \le 24N\)
Phương án B: \(6N \le F \le 26N\)
Phương án C: \(30N \le F \le 62N\)
Phương án D: \(34N \le F \le 66N\)
=> Lực có môđun 30N là hợp lực của hai lực thành phần 16N và 46N có cùng phương nhưng ngược chiều
Câu hỏi 23 :
Một vật khối lượng \(2,5kg\) đang nằm yên trên mặt phẳng nằm ngang thì chịu tác dụng của lực kéo \(15N\) theo phương ngang và bắt đầu chuyển động. Biết trong 1 phút đầu tiên sau khi chịu tác dụng lực, vật đi được \(2700m\). Coi lực cản tác dụng vào vật không đổi trong quá trình chuyển động. Lực cản tác dụng vào vật bằng:
- A
11,25N
- B
13,5N
- C
9,75N
- D
15,125N
Đáp án: A
Phương pháp giải:
+ Vận dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \)
+ Vận dụng biểu thức xác định quãng đường: \(S = {v_0}t + \dfrac{1}{2}a{t^2}\)
Lời giải chi tiết:
Đổi : \(1 \text{phút} = 60 s\)
Ta có: \(S = {v_0}t + \dfrac{1}{2}a{t^2}\)
\( \to a = \dfrac{{2S}}{{{t^2}}} = \dfrac{{2.2700}}{{{{60}^2}}} = 1,5m/{s^2}\)
Lực cản tác dụng vào vật bằng:
\(F - {F_C} = ma \\\to {F_C} = F - ma \\= 15 - 2,5.1,5 = 11,25N\)
Câu hỏi 24 :
Dưới tác dụng của một lực \(20N\) thì một vật chuyển động với gia tốc $0,4m/{s^2}$ . Nếu tác dụng vào vật này một lực \(50N\) thì vật này chuyển động với gia tốc bằng:
- A
$1m/{s^2}$
- B
$0,5m/{s^2}$
- C
$2m/{s^2}$
- D
$4m/{s^2}$
Đáp án: A
Phương pháp giải:
Áp dụng định luật II Niutơn: \(\overrightarrow F = m\overrightarrow a \)
Lời giải chi tiết:
Áp dụng định luật II Niutơn ta có: \(a = \dfrac{F}{m} \to m = \dfrac{F}{a} = \dfrac{{20}}{{0,4}} = 50kg\)
Nếu tác dụng vào vật một lực thì vật này chuyển động với gia tốc bằng: \(a = \dfrac{F}{m} = \dfrac{{50}}{{50}} = 1m/{s^2}\)
Câu hỏi 25 :
Biết sao Hỏa có bán kính bằng 0,53 bán kính Trái Đất và có khối lượng bằng 0,1 lần khối lượng Trái Đất. Một vật có gia tốc rơi tự do ở trên mặt đất là $9,8m/{s^2}$, nếu vật này rơi tự do trên sao Hỏa thì gia tốc rơi là
- A
$3,5m/{s^2}$
- B
$7,0m/{s^2}$
- C
$2,8m/{s^2}$
- D
$3,25m/{s^2}$
Đáp án: A
Phương pháp giải:
Vận dụng biểu thức xác định gia tốc trọng trường (gia tốc rơi tự do): $g = G\dfrac{M}{{{{\left( {R \pm h} \right)}^2}}}$
Lời giải chi tiết:
Từ đầu bài, ta có:
$\left\{ \begin{array}{l}
{M_{SH}} = 0,1{M_{T{\rm{D}}}}\\
{R_{SH}} = 0,53{{\rm{R}}_{TD}}
\end{array} \right.$
và gia tốc trọng trường trên mặt đất $g = 9,8m/{s^2}$
Câu hỏi 26 :
Hai vệ tinh nhân tạo I và II bay quanh Trái Đất trên quỹ đạo tròn bán kính lần lượt là \(r\) và \(2r\). Tốc độ của vệ tinh I là \({v_1}\). Hỏi tốc độ \({v_2}\) của vệ tinh II là bao nhiêu?
- A \(2{v_1}\)
- B \({v_1}\)
- C \(\dfrac{{{v_1}}}{{\sqrt 2 }}\)
- D \(\dfrac{{{v_1}}}{2}\)
Đáp án: C
Phương pháp giải:
+ Lực hấp dẫn: \({F_{hd}} = \dfrac{{G.{m_1}{m_2}}}{{{r^2}}}\)
+ Lực hướng tâm: \({F_{ht}} = m.\dfrac{{{v^2}}}{r}\)
Lời giải chi tiết:
Ta có lực hấp dẫn giữa vệ tinh và trái đất đóng vai trò là lực hướng tâm.
\({F_{ht}} = {F_{hd}} \Leftrightarrow \dfrac{{m{v^2}}}{r} = \dfrac{{G.mM}}{{{r^2}}} \Rightarrow v = \sqrt {\dfrac{{GM}}{r}} \)
Tỉ số tốc độ của hai vệ tinh là:
\(\dfrac{{{v_2}}}{{{v_1}}} = \dfrac{{\sqrt {\dfrac{{GM}}{{{r_2}}}} }}{{\sqrt {\dfrac{{GM}}{{{r_1}}}} }} = \sqrt {\dfrac{{{r_1}}}{{{r_2}}}} = \sqrt {\dfrac{r}{{2r}}} = \dfrac{1}{{\sqrt 2 }} \Rightarrow {v_2} = \dfrac{{{v_1}}}{{\sqrt 2 }}\)
Câu hỏi 27 :
Cho cơ hệ như hình vẽ:
- A
15 J
- B
1,5 J
- C
30J
- D
3,0 J
Đáp án: A
Phương pháp giải:
- Sử dụng công thức tính công: \(A = mgh\)
Lời giải chi tiết:
Khi \({m_1}\) đi lên quãng đường \(s = 1m\) trên mặt phẳng nghiêng thì \({m_2}\)đi xuống thẳng đứng một quãng đường cũng băng s (hình vẽ)
Câu hỏi 28 :
Hai mặt phẳng đỡ tạo với mặt phẳng nằm ngang các góc α = 45o . Trên hai mặt phẳng đó người ta đặt một quả cầu đồng chất có khối lượng 2 kg (Hình 17.10). Bỏ qua ma sát và lấy g = 10 m/s2. Hỏi áp lực của quả cầu lên mỗi mặt phẳng đỡ bằng bao nhiêu?
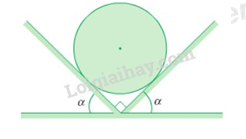
- A 20 N
- B 28 N
- C 14 N
- D 1,4 N
Đáp án: C
Phương pháp giải:
Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng 0:
\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + ... = \overrightarrow 0 \)
Lời giải chi tiết:
Lực tác dụng lên quả cầu được biểu diễn như hình vẽ.

Khi hệ cân bằng ta có: \(\overrightarrow P + \overrightarrow {{N_1}} + \overrightarrow {{N_2}} = \overrightarrow 0 \,\,\,\,\left( 1 \right)\)
Chọn hệ trục toạ độ Oxy như hình vẽ.
Chiếu phương trình (1) lên các trục Ox, Oy ta có :
\(\begin{array}{l}\left\{ \begin{array}{l}{N_1}.\cos \alpha - {N_2}.\cos \alpha = 0\\ - P + {N_1}.\sin \alpha + {N_2}.\sin \alpha = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{N_1} = {N_2}\\P = {N_1}.\sin \alpha + {N_2}.\sin \alpha \end{array} \right. \Rightarrow P = 2{N_1}\sin \alpha \\ \Rightarrow {N_1} = \dfrac{P}{{2\sin \alpha }} = \dfrac{{mg}}{{2\sin \alpha }} = \dfrac{{2.10}}{{2.\sin 45}} \approx 14N \Rightarrow {N_1} = {N_2} = 14N\end{array}\)
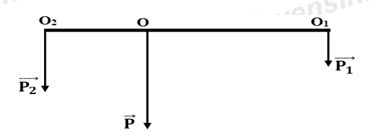
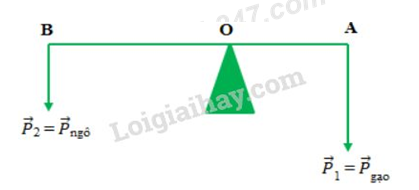
Câu hỏi 29 :
Một người gánh hai thúng, một thúng gạo nặng 300N, một thúng ngô nặng 200N. Đòn gánh dài 1,5m. Hỏi vai người này phải đặt ở điểm nào để đòn gánh cân bằng và vai chịu một lực bằng bao nhiêu? Bỏ qua trọng lượng của đòn gánh.
- A Vai người chịu tác dụng của 1 lực 250N; Vai người đặt tại điểm cách đầu treo thúng gạo 60cm
- B Vai người chịu tác dụng của 1 lực 500N; Vai người đặt tại điểm cách đầu treo thúng gạo 60cm
- C Vai người chịu tác dụng của 1 lực 500N; Vai người đặt tại điểm cách đầu treo thúng gạo 90cm
- D Vai người chịu tác dụng của 1 lực 250N; Vai người đặt tại điểm cách đầu treo thúng gạo 90cm
Đáp án: B
Phương pháp giải:
Quy tắc tổng hợp hai lực song song cùng chiều:
- Hợp lực của hai lực song song cùng chiều là một lực song song, cùng chiều và có độ lớn bằng tổng các độ lớn của hai lực ấy.
- Giá của hợp lực chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy.
\(F = {F_1} + {F_2};\dfrac{{{F_1}}}{{{F_2}}} = \dfrac{{{d_2}}}{{{d_1}}}\) (chia trong)
Lời giải chi tiết:
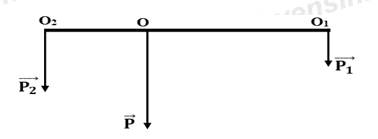
Trọng lượng của gạo là: P1 = 300N
Trọng lượng của gạo là: P2 = 200N
Vai người chịu tác dụng của một lực:
P = P1 + P2 = 300 + 200 = 500N
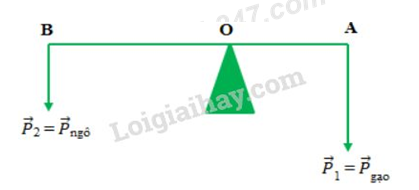
Ta có: \(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{O{O_2}}}{{O{O_1}}} = \dfrac{{300}}{{200}} = \dfrac{3}{2} \Rightarrow 3.O{O_1} - 2.O{O_2} = 0\,\,\,\left( 1 \right)\)
Lại có: \(O{O_1} + O{O_2} = AB = 150cm\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}3.O{O_1} - 2.O{O_2} = 0\\O{O_1} + O{O_2} = 150cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}O{O_1} = 60cm\\O{O_2} = 90cm\end{array} \right.\)
Vậy vai người gánh chịu một lực là P = 500 (N), điểm đặt của vai cách đầu treo thúng gạo một khoảng 60 cm.
Câu hỏi 30 :
Xe khối lượng \(1\) tấn chuyển động thẳng đều lên dốc dài \(200m\), cao \(10m\) với vận tốc \(18km/h\). Biết hệ số ma sát có giá trị \(0,01\). Xác định lực kéo của động cơ để xe có trạng thái nêu trên
- A \(600N\)
- B \(500N\)
- C \(200N\)
- D \(100N\)
Đáp án: A
Phương pháp giải:
+ Công thức tính lực ma sát: \({F_{ms}} = \mu N\)
+ Phương trình định luật II Niuton: \(\sum {\overrightarrow F } = m.\overrightarrow a \,\,\,\,\left( * \right)\)
Chiếu (*) lên Ox và Oy.
+ Định luật I Niu - tơn: Nếu không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không, thì vật đang đứng yên sẽ tiếp tục đứng yên, đang chuyển động sẽ tiếp tục chuyển động thẳng đều.
Lời giải chi tiết:

Chọn hệ trục tọa độ như hình vẽ:
Áp dụng định luật II Newton:
\(\overrightarrow {F_{ms}} + \overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a \Leftrightarrow \overrightarrow {F_{ms}} + \overrightarrow P + \overrightarrow N + \overrightarrow F_1 + \overrightarrow F_2 = m.\overrightarrow a\,\,\,\left ( * \right )\)
Chiếu phương trình (*) lên Ox, Oy, ta có:
\(\left\{ \begin{array}{l}N = P_2 = P.\cos \alpha = mg\cos \alpha \\F - F_{ms} - P_1 = 0\Leftrightarrow F - \mu N - mg\sin \alpha = 0 \end{array} \right.\)
(do xe chuyển động thẳng đều)
\(\begin{array}{l} \Rightarrow F = \mu N + mg\sin \alpha = \mu mg\cos \alpha + mg\sin \alpha \\\,\,\,\,\,\,\,\,\,\,\, = mg.\left( {\mu \cos \alpha + \sin \alpha } \right)\\\,\,\,\,\,\,\,\,\,\,\, = {10^3}.10.\left( {0,01.\dfrac{{\sqrt {{{200}^2} - {{10}^2}} }}{{200}} + \dfrac{1}{{20}}} \right) = 600N\end{array}\)
