Câu 1 (2,5 điểm):
a) Phát biểu và viết công thức của định luật Cu-lông.
b) Viết công thức tính cường độ điện trường của một điện tích điểm.
Câu 2 (2,0 điểm):
a) Nêu bản chất của dòng điện trong kim loại và dòng điện trong chất điện phân.
b) Phát biểu định nghĩa và viết công thức tính điện dung của tụ điện.
Câu 3 (2,5 điểm):
Một điện tích điểm \({q_1} = + {9.10^{ - 6}}C\) đặt tại điểm O trong chân không. Xét điểm M nằm cách \({q_1}\) một khoảng 20cm.
a) Tính độ lớn của cường độ điện trường do điện tích điểm \({q_1}\) gây ra tại điểm M.
b) Người ta đặt tại M một điện tích điểm \({q_2} = + 4\mu C\). Tính độ lớn của lực điện trường tác dụng lên điên tích \({q_2}\).
Câu 4 (3,0 điểm):
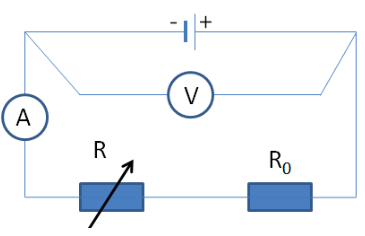
Trong giờ thực hành một học sinh mắc một mạch điện như hình vẽ. Biết các dụng vụ đo lý tưởng, R là một biến trở. Suất điện động và điện trở trong lần lượt là \(\xi = 12V,\,\,\,r = 3\Omega \), điện trở \({R_0} = 5\Omega \).
1. Lúc đầu học sinh này điều chỉnh con chạy của biến trở để \(R = 0\).
a) Tính cường độ dòng điện trong mạch.
b) Tính công suất của nguồn điện.
c) Tính nhiệt lượng tỏa ra trên điện trở \({R_0}\) trong thời gian 1 phút.
2. Sau đó học sinh này thay nguồn điện, thay điện trở \({R_0}\) và điều chỉnh biến trở \(R\). Biết rằng:
Khi \(R = {R_1}\), vôn kế chỉ 5V, ampe kế chỉ 1A.
Khi \(R = {R_2}\), vôn kế chỉ 4V, ampe kế chỉ 2A.
Xác định suất điện động và điện trở trong của nguồn điện.
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn soanvan.me
Câu 1 (NB):
Phương pháp:
a) Sử dụng lí thuyết về định luật Cu-lông SGK VL11 trang 9
b) Sử dụng lí thuyết về cường độ điện trường của một điện tích điểm SGK VL11 trang 17
Cách giải:
a) Định luật Cu-lông:
Lực hút hay đẩy giữa hai điện tích điểm đặt trong chân không có phương trùng với đường thẳng nối hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
Công thức: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) với \(k = {9.10^9}\frac{{N.{m^2}}}{{{C^2}}}\)
b) Cường độ điện trường của một điện tích điểm: \(E = \frac{F}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)
Câu 2 (TH):
Phương pháp:
a) Sử dụng lí thuyết về dòng điện trong kim loại và dòng điện trong chất điện phân
b) Sử dụng lí thuyết về tụ điện SGK VL11 trang 30
Cách giải:
a)
- Dòng điện trong kim loại: Dòng điện trong kim loại là dòng dịch chuyển có hướng của các êlectron tự do ngược chiều điện trường.
- Dòng điện trong chất điện phân: Dòng điện trong chất điện phân là dòng chuyển dời có hướng của các ion dương theo chiều điện trường và các ion âm ngược chiều điện trường.
b)
- Định nghĩa: Tụ điện là một hệ hai vật dẫn đặt gần nhau và ngăn cách nhau bằng một lớp cách điện.
- Công thức: \(C = \frac{Q}{U}\)
Câu 3 (VD):
Phương pháp:
a) Vận dụng biểu thức: \(E = k\frac{{\left| Q \right|}}{{{r^2}}}\)
b) Sử dụng biểu thức định luật Cu-lông: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\) hoặc \(F = qE\)
Cách giải:
a) Cường độ điện trường do điện tích \({q_1}\) gây ra tại M: \(E = k\frac{{\left| {{q_1}} \right|}}{{{r^2}}} = {9.10^9}\frac{{\left| {{{9.10}^{ - 6}}} \right|}}{{0,{2^2}}} = 20,{25.10^5}V/m\)
b) Lực điện trường tác dụng lên \({q_2}\) là: \(F = {q_2}E = {4.10^{ - 6}}.20,{25.10^5} = 8,1N\)
Câu 4 (VD):
Phương pháp:
1.
a) Sử dụng biểu thức định luật Ôm cho toàn mạch: \(I = \frac{E}{{R + r}}\)
b) Sử dụng biểu thức tính công suất: \(P = EI\)
c) Sử dụng biểu thức tính nhiệt lượng: \(Q = {I^2}Rt\)
2. Sử dụng biểu thức định luật Ôm
Cách giải:
1.
a. Cường độ dòng điện trong mạch: \(I = \frac{E}{{{R_0} + r}} = \frac{{12}}{{5 + 3}} = 1,5A\)
b. Công suất của nguồn điện: \(P = EI = 12.1,5 = 18W\)
c. Nhiệt lượng tỏa ra trên \({R_0}\) trong thời gian \(t = 1' = 60s\) là: \(Q = {I^2}{R_0}t = 1,{5^2}.5.60 = 675J\)
2.
Cường độ dòng điện trong mạch: \(I = \frac{E}{{R + {R_0} + r}}\)
Số chỉ của vôn kế: \({U_V} = E - Ir\)
+ Khi \(R = {R_1}\):
\(\begin{array}{l}\left\{ \begin{array}{l}{I_1} = 1A\\{U_{{V_1}}} = 5V\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = \frac{E}{{{R_1} + 5 + r}}\\5 = E - \frac{E}{{{R_1} + 5 + r}}r\end{array} \right.\\ \Rightarrow E - r = 5{\rm{ }}\left( 1 \right)\end{array}\)
+ Khi \(R = {R_2}\):
\(\begin{array}{l}\left\{ \begin{array}{l}{I_2} = 2A\\{U_{{V_2}}} = 4V\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 = \frac{E}{{{R_2} + 5 + r}}\\4 = E - \frac{E}{{{R_2} + 5 + r}}r\end{array} \right.\\ \Rightarrow E - 2r = 4{\rm{ }}\left( 2 \right)\end{array}\)
Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}E = 6V\\r = 1\Omega \end{array} \right.\)
soanvan.me
