Đề bài
Tam giác A’B’C’ đồng dạng với tam giác ABC, tỉ số đồng dạng \(k = {{B'C'} \over {BC}}\) (hình 29).
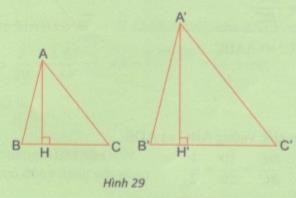
Viết công thức tính diện tích \({S_1}\) ứng với đường cao A’H’ của tam giác A’B’C’.
Viết công thức tính diện tích \({S_2}\) ứng với đường cao AH của tam giác ABC.
Lập tỉ số \({{{S_1}} \over {{S_2}}}\) . Em có nhận xét gì về tỉ số \({{{S_1}} \over {{S_2}}}\) với tỉ số đồng dạng k ?
Lời giải chi tiết
Ta có \({S_1} = {1 \over 2}B'C'.A'H',{S_2} = {1 \over 2}BC.AH\)
\(\Rightarrow {{{S_1}} \over {{S_2}}} = {{{1 \over 2}B'C'.A'H'} \over {{1 \over 2}BC.AH}} = {{B'C'.A'H'} \over {BC.AH}}\)
\({{{S_1}} \over {{S_2}}} = {{B'C'} \over {BC}}.{{A'H'} \over {AH}} = k.k = {k^2}\)
soanvan.me
