Đề bài
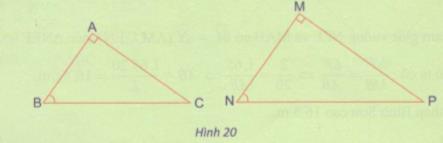
a) Từ trường hợp đồng dạng thứ ba (g.g) của hai tam giác, xét xem hai tam giác vuông ABC và MNP có \(\widehat B = \widehat N\) có đồng dạng với nhau không ?
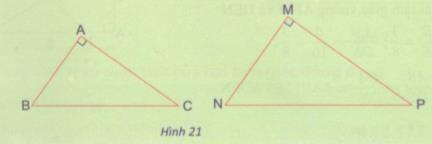
b) Từ trường hợp đồng dạng thứ hai (c.g.c) của hai tam giác, xét xem nếu tam giác vuông ABC và MNP có \({{AB} \over {MN}} = {{AC} \over {MP}}\) thì hai tam giác đó có đồng dạng với nhau không ?
Lời giải chi tiết
a) Xét ∆ABC và ∆MNP có: \(\widehat A = \widehat M( = 90^\circ ),\widehat B = \widehat N(gt)\)
\(\Rightarrow \Delta ABC \sim \Delta MNP(g.g)\)
b) Xét ∆ABC và ∆MNP có \({{AB} \over {MN}} = {{AC} \over {MP}}(gt),\widehat A = \widehat M( = 90^\circ ) \)
\(\Rightarrow \Delta ABC \sim \Delta MNP(c.g.c)\)
soanvan.me
