Đề bài
Cho tam giác ABC (hình 2) với giả thiết và kết luận như sau :
|
GT |
Tam giác ABC AC >AB |
|
KL |
\(\widehat B > \widehat C\) |
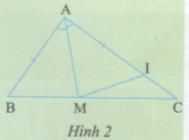
Vẽ tia phân giác AM của góc A (M thuộc BC). Trên tia AC, lấy điểm I sao cho AI = AB. Vì AC > AB nên điểm I nằm giữa A và C.
Hãy điền vào chỗ trống cho thích hợp :
Xét tam giác ABM và AIM, ta có :
AB = …..(……………………………………..)
\(...... = \widehat {MAI}(............................................)\)
AM là ….
Vậy tam giác ……. = tam giác ……… (…………………………….)
\( \Rightarrow\) góc ………. = góc AIM.
Mà góc AIM là góc ngoài của tam giác MIC nên góc AIM …….. góc C.
\( \Rightarrow\) góc B ….. góc C.
Lời giải chi tiết
Xét tam giác ABM và AIM, ta có :
AB = AI (Trên tia AC lấy I sao cho AI = AB),
\(\widehat {BAM} = \widehat {MAI}\) (AM là tia phân giác \(\widehat A\)) và AM là cạnh chung
Vậy tam giác ABM = tam giác AIM (c.g.c) => góc ABM = góc AIM.
Mà góc AIM là góc ngoài của tam giác MIC nên góc AIM > góc C => góc B > góc C.
soanvan.me
