Đề bài
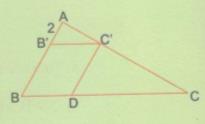
Cho tam giác ABC có AB = 6cm, AC = 8 cm và BC = 10 cm.
Lấy điểm B’ trên AB sao cho AB’ = 2 cm, qua B’ vẽ đường thẳng song song với BC và cắt AC tại C’.
a) Tính AC’
b) Qua C’ vẽ đường thẳng song song với AB và cắt BC tại D. Tính BD, B’C’.
c) Tính và so sánh các tỉ số: \({{AB'} \over {AB}}\,\,,\,\,{{AC'} \over {AC}}\,\,,\,\,{{B'C'} \over {BC}}\)
Lời giải chi tiết
a) ∆ABC có \(B'C'//BC(gt)\)
\(\Rightarrow \dfrac{{AC'}}{{AC}} = \dfrac{{AB'}}{{AB}}\) (Định lí Thales)
Do đó \(\dfrac{{AC'}}{8} = \dfrac{2}{6} \Rightarrow AC' = \dfrac{2}{6}.8 = \dfrac{8}{3}(cm)\)
b) ∆ABC có \(C'D//AB(gt)\)
\(\Rightarrow \dfrac{{BD}}{{BC}} = \dfrac{{AC'}}{{AC}}\) (Định lí Thales)
Do đó \(\dfrac{{B{\text{D}}}}{{10}} = \dfrac{{\dfrac{8}{3}}}{8} \Rightarrow BD = \dfrac{1}{3}.10 = \dfrac{{10}}{3}(cm)\)
Tứ giác BB’C’D có BB’//DC’, B’C’//BD
\( \Rightarrow \) Tứ giác BB’C’D là hình bình hành \( \Rightarrow B'C' = BD = \dfrac{10}{ 3}(cm)\)
c)
\(\dfrac{{AB'}}{{AB}} = \dfrac{2}{6} = \dfrac{1}{3};\)
\(\dfrac{{AC'}}{{AC}} = \dfrac{{\dfrac{8}{3}}}{8} = \dfrac{1}{3};\)
\(\dfrac{{B'C'}}{{BC}} = \dfrac{{\dfrac{{10}}{3}}}{{10}} = \dfrac{1}{3}\)
Vậy \(\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}} = \dfrac{{BC'}}{{BC}}\)
soanvan.me
