Đề bài
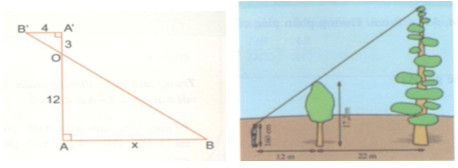
a) Hãy chứng minh AB // A’B’ và tính độ dài AB trong hình dưới.
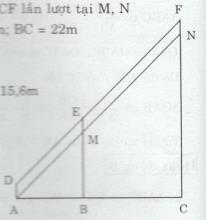
b) Hãy tính chiều cao của cây cao nhất trong hình vẽ dưới đây.
Lời giải chi tiết
a)\(AB \bot AA'(gt),A'B' \bot AA'(gt)\)
\(\Rightarrow AB//A'B'\)
∆OAB có AB // A’B’ \( \Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{OA'}}{{OA}}\) (Hệ quả của định lí Thales)
Nên \(\dfrac{4}{x} = \dfrac{3}{{12}} \)\(\;\Rightarrow x = \dfrac{{4.12}}{3} = 16\)
b) Đặt tên các vị trí như như hình bên
Qua A vẽ đường thẳng song song với DE, cắt BE, CF lần lượt tại M, N
Ta có \(AD =160cm = 1,6m; BE = 17,2m; \)\(\,AB = 12m; BC = 22m\)
Do đó AC = AB + BC = 34m
Các tứ giác ADEM, MEFN là hình bình hành
Nên \(EM = FN = AD = 1,6m \)
\(\Rightarrow BM = BE – EM = 15,6m\)
∆CAN có BM//CN
\(\dfrac{{BM}}{{CN}} = \dfrac{{AB}}{{AC}}\) (Hệ quả của định lí Thales)
Nên \(\dfrac{{15,6}}{{CN}} = \dfrac{{12}}{{34}}\)
\(\Rightarrow CN = \dfrac{{15,6.12}}{{34}} = 44,2(m)\)
\( \Rightarrow CF = CN + FN = 44,2 + 1,6 \)\(\,= 45,8(m)\)
Vậy chiều cao của cây cao nhất trong hình vẽ là 45,8 m
soanvan.me
