1. Hàm số
+ Nếu đại lượng $y$ phụ thuộc vào đại lượng $x$ sao cho với mỗi giá trị của $x$ ta luôn xác định được chỉ một giá trị tương ứng của $y$ thì $y$ được gọi là hàm số của $x$ và $x$ được gọi là biến số.
+ Hàm số thường được cho bằng bảng hoặc bằng công thức.
+ Tập hợp tất cả các điểm biểu diễn các tập giá trị tương ứng $\left( {x;{\rm{ }}f\left( x \right)} \right)\; $trên mặt phẳng tọa độ $Oxy$ được gọi là đồ thị của hàm số.
+ Tính đồng biến và nghịch biến của hàm số:
Cho hàm số $y = f\left( x \right)$ xác định với mọi giá trị với bất kì thuộc $D:$
+) Nếu ${x_1} < {x_2}$ mà $f({x_1}) < f({x_2})$ thì hàm số đồng biến trên $D.$
+) Nếu ${x_1} < {x_2}$ mà $f({x_1}) > f({x_2})$ thì hàm số nghịch biến trên $D.$
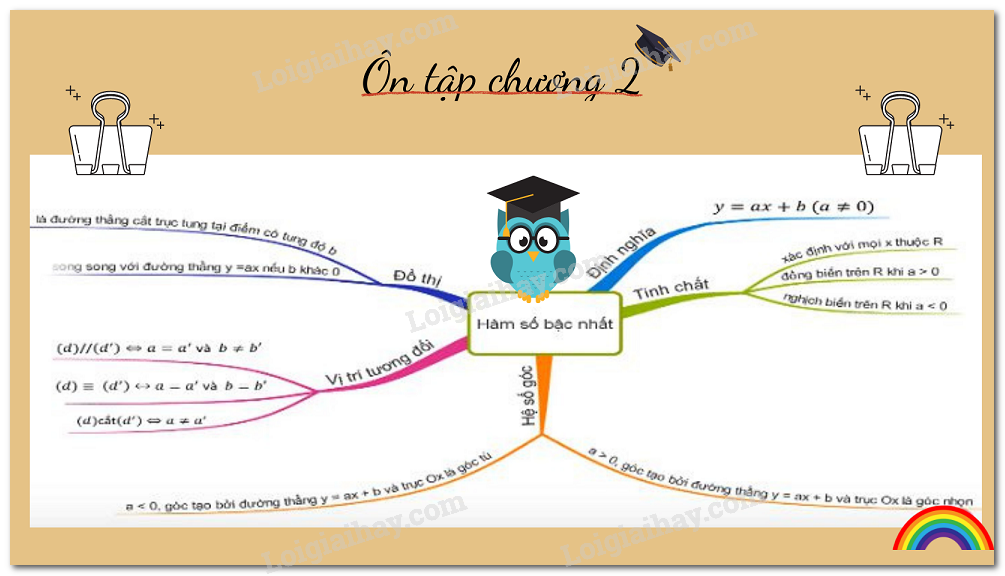
2. Hàm số bậc nhất
+ Hàm số bậc nhất là hàm số được cho bởi công thức $y{\rm{ }} = {\rm{ }}ax{\rm{ }} + {\rm{ }}b$ trong đó $a,b$ là các số cho trước và $a \ne 0$.
+ Hàm số bậc nhất xác định với mọi giá trị và:
- Đồng biến trên $\mathbb{R}$ khi $a > 0. $
- Nghịch biến trên $\mathbb{R}$ khi $a < 0.$
+ Đồ thị của hàm số bậc nhất $y = ax + b{\rm{ }}(a \ne 0)$ là một đường thẳng và $a$ là hệ số góc của đường thẳng.
+ Cho hai đường thẳng $y = {a_1}x + {b_1}({a_1} \ne 0);y = {a_2}x + {b_2}({a_2} \ne 0)$
Ta có:
+) ${d_1};{d_2}$ song song $ \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right.$.
+) ${d_1};{d_2}$ trùng nhau $ \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} = {b_2}\end{array} \right.$.
+) ${d_1};{d_2}$ cắt nhau $ \Leftrightarrow {a_1} \ne {a_2}$.
+) ${d_1};{d_2}$ vuông góc với nhau $ \Leftrightarrow {a_1}.{a_2} = - 1$.