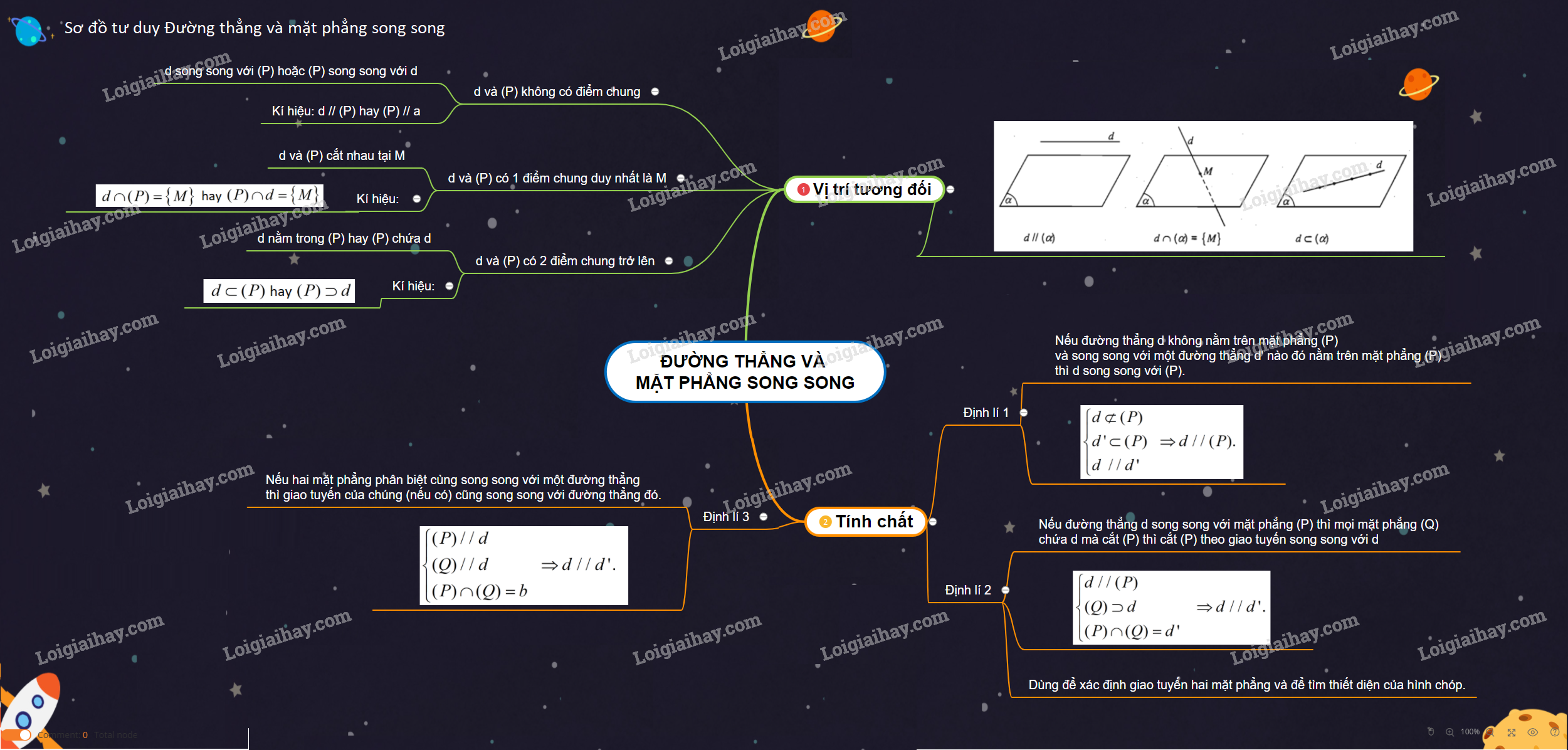
- Nếu đường thẳng \(a\) không nằm trên mặt phẳng \((P)\) và song song với một đường thẳng \(b\) nào đó nằm trên mặt phẳng \((P)\) thì \(a\) song song với \((P)\).
Kí hiệu:
\(\left\{ \begin{array}{l}
a \not\subset (P)\\
b \subset (P)\\
a\,\;//\;b
\end{array} \right.\;\;\; \Rightarrow a\;//\;(P).\)
- Nếu đường thẳng \(a\) song song với mặt phẳng \((P)\) thì mọi mặt phẳng \((Q)\) chứa \(a\) mà cắt \((P)\) thì cắt \((P)\) theo giao tuyến song song với \(a\). (Đây là tính chất quan trọng dùng để xác định giao tuyến hai mặt phẳng và để tìm thiết diện của hình chóp).
Kí hiệu:
\(\left\{ \begin{array}{l}
a\;//\;(P)\\
(Q) \supset a\\
(P) \cap (Q) = b
\end{array} \right.\;\;\;\; \Rightarrow a\;//\;b.\)
- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Kí hiệu:
\(\left\{ \begin{array}{l}
(P)//\;a\\
(Q)//\;a\\
(P) \cap (Q) = b
\end{array} \right.\;\;\; \Rightarrow a\;//\;b.\)
- Nếu \(a\) và \(b\) là hai đường thẳng chéo nhau thì có duy nhất một mặt phẳng chứa \(a\) và song song với \(b\).
soanvan.me
