Bài toán:
Cho đường thẳng \(d\) và mặt phẳng \(\left( P \right)\). Tìm giao điểm của \(d\) và \(\left( P \right)\).
Phương pháp:
Cách 1:
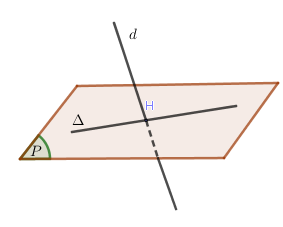
- Bước 1: Tìm một đường thẳng \(\Delta \) nằm trong \(\left( P \right)\) mà \(d\) cắt \(\Delta \).
- Bước 2: Giao điểm của \(d\) và \(\Delta \) chính là giao điểm của \(d\) và \(\left( P \right)\).
Cách 2:
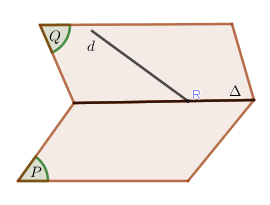
- Bước 1: Tìm mặt phẳng \(\left( Q \right) \supset d\) mà \(\left( Q \right) \cap \left( P \right) = \Delta \).
- Bước 2: Giao điểm của \(d\) và \(\Delta \) chính là giao điểm của \(d\) và \(\left( P \right)\).
Ví dụ: Cho bốn điểm \(A,B,C,D\) không đồng phẳng. Trên \(AD,AB\) lần lượt lấy các điểm \(E,F\) sao cho \(EF\) không song song \(BD\). Tìm giao điểm của đường thẳng \(EF\) và mặt phẳng \(\left( {BCD} \right)\).
Giải:
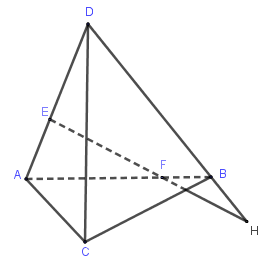
Gọi \(H\) là giao điểm của \(EF\) và \(BD\).
Do đó \(H \in BD \Rightarrow H \in \left( {BCD} \right)\), mà \(H \in EF\) nên \(H = EF \cap \left( {BCD} \right)\).
